|
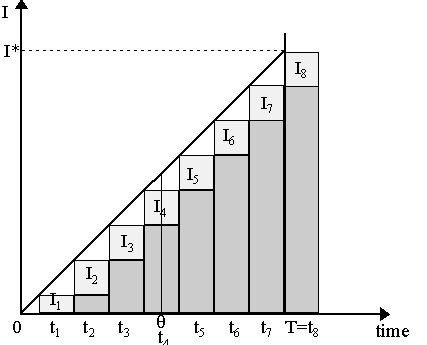
William Stanley Jevons (1871: Ch. VII) was one of the first to conceive of capital as being characterized as time. More specifically, capital is "the aggregate of those commodities which are required for sustaining labourers of any kind or class engaged in work...The single and all-important function of capital is to enable the laborer to await the result of any long-lasting work, -- to put an interval between the beginning and the end of an enterprise" (Jevons, 1871: p.223). Thus, for Jevons, capital is merely a subsistence fund that goes into maintaining the labor inputs working on the production of goods whose fruit will only emerge in a later time. Jevons (1871: p.229) distinguishes between "the amount of capital invested" and the "amount of investment of capital". The difference between these two concepts is subtly worded but nonetheless substantial. The "amount of capital invested" is the "physical quantity" of inputs into the production process while the "amount of investment in capital" is that physical quantity of inputs multiplied by the length of time in which each input has been in the production process. To understand this, consider Figure 1 where we have plotted time against increments of input additions. Consider a process of production which begins at time t0 and ends at time t8. This is what Ragnar Frisch (that lord of economic nomenclature!) called a "flow-input, point-output" situation: where inputs are added over time to a production process until a particular final time period, when all the output is realized at once. The histogram in Figure 1 represents the "lumpy" addition of inputs into this process over (discrete) time. The addition in any period is represented by the lightly shaded rectangles. Thus, at t0, we implement amount I0 of inputs into the process, at time t1, we add I1 worth of inputs, and so on until the final time period t8 where we add I8 worth of inputs and our production process ends. Time t8, the final time period, is when output is finally realized.
If we were in continuous time, then our addition of inputs would be continuous until the final time period. This is represented heuristically in Figure 1 by the straight diagonal line stretching from the origin (not perfectly drawn). We begin at time t = 0 and end at time t = T, adding inputs continuously and, in the final time period, have I* worth of inputs "stored" in the production process. What is the quantity of capital? According to Jevons, the "amount of capital invested" is merely the sum of all the inputs during the production process - or the sum of the heights of the lightly-shaded rectangles in our figure. In Figure 1, this adds up to I*, i.e. I* = I1 + I2 + .. + I8 in discrete time. In general, for discrete time production process from an initial time period t = 0 to a final time period t = T:
However, what Jevons called the "amount of investment of capital" is the sum of the inputs multiplied by the length of time of production - thus it is the entire area of the histogram, or the entire area of the triangle formed by the production process. Thus:
which is the area of the histogram in Figure 1. What about in continuous time? In this case, the amount of capital invested is simply I* = ˛ 0T I(t) dt where I(t) is the investment rate. For the amount of investment in capital, it is useful to appeal to what Jevons called the "average time of investment" (Jevons, 1871: p.231) which is simple the average of the production period, which can be defined in continuous time as q = T/2 as shown in Figure 1. With the average time of investment so defined, then the "amount of investment of capital" can be expressed as q I* = TI*/2 - which is, as we see, the precisely the area of the triangle depicted in Figure 1. This "amount of investment of capital" is, quite simply, the measurement of the quantity of capital for Jevons - a concept quite similar to that derived from the "average period of production" of Eugen von B÷hm-Bawerk (1889). |
All rights reserved, Gonšalo L. Fonseca