|
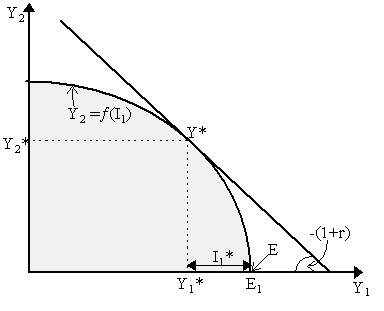
Irving Fisher's theory of capital and investment was introduced in his Nature of Capital and Income (1906) and Rate of Interest (1907), although it has its clearest and most famous exposition in his Theory of Interest (1930). We shall be mostly concerned with what he called his "second approximation to the theory of interest" (Fisher, 1930: Chs.6-8), which sets the investment decision of the firm as an intertemporal problem. In his theory, Fisher assumed (note carefully) that all capital was circulating capital. In other words, all capital is used up in the production process, thus a "stock" of capital K did not exist. Rather, all "capital" is, in fact, investment. Friedrich Hayek (1941) would later take him to task on this assumption - in particular, questioning how Fisher could reconcile his theory of investment with the Clarkian theory of production which underlies the factor market equilibrium. Given that Fisher's theory output is related not to capital but rather to investment, then we can posit a production function of the form Y = ¦ (N, I). Now, Fisher imposed the condition that investment in any time period yields output only in the next period. For simplicity, let us assume a world with only two time periods, t = 1, 2. In this case, investment in period 1 yields output in period 2 so that Y2 = ¦ (N, I1) where I1 is period 1 investment and Y2 is period 2 output. Holding labor N constant (and thus striking it out of the system), then the investment frontier can be drawn as the concave function where ¦ ¢ > 0 and ¦ ¢ ¢ < 0. The mirror image of this is shown in Figure 1 as the frontier Y2 = ¦ (I1). Everything below this frontier is technically feasible and everything above it is infeasible. Letting r be the rate of interest then total costs of investing an amount I1 is (1+r)I1. Similarly, total revenues are derived from the sale of output pY2 or, normalizing p = 1, simply Y2. Thus, profits from investment are defined as p = Y2 - (1+r)I1 and the firm faces the constraint Y2 = ¦ (I1) (we have omitted N now). Thus, the firm's profit-maximization problem can be written as:
so that the optimal investment decision will be where:
In Fisher's language, we can define ¦ ¢ -1 as the "marginal rate of return over cost", or in more Keynesian language, the "marginal efficiency of investment", so MEI = ¦ ¢ - 1. Thus, the optimum condition for the firm's investment decision is that MEI = r, i.e. marginal efficiency of investment is equated with rate of interest. Obviously, as ¦ (I1) is a concave function, then as I1 rises, ¦ ¢ declines. As the rate of interest rises, then to equate r and MEI, it must be that investment declines - thus the negative relationship between investment and interest rate. Succinctly, I = I(r) where Ir = dI/dr < 0.
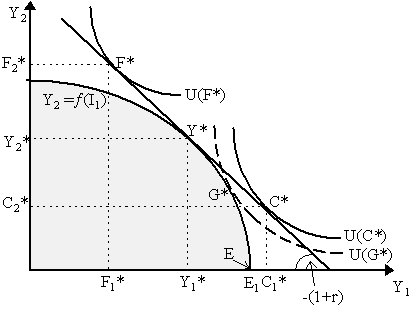
In Figure 1, we have drawn Fisher's investment frontier Y2 = ¦ (I1) where the concave nature of the curve reflects, of course, diminishing marginal returns to investment. Suppose we start at initial endowment of intertemporal output E - where E1 > 0 and E2 = 0, so we only have endowment in period 1. Then the amount of "investment" involves allocating some amount of period 1 endowment to production for period 2. The output left over for period 1 consumption, let us call that Y1*, is effectively the amount of intitial endowment that investment has not appropriated, i.e. Y1* = E1 - I1*. The investment decision will be optimal where the investment frontier is tangent to the interest rate line, i.e. where ¦ ¢ = (1+r). At this point, intertemporal allocation of income becomes Y* = (Y1*, Y2*) where Y2* = ¦ (I1*) and Y1* = E1 - I1*. It is obvious, by playing with this diagram, that as r increases (interest rate line becomes steeper), then I1* declines; whereas as r declines (interest line becomes flatter), then I1* increases. Thus, dI/dr < 0, so investment is negatively related to the interest rate. So far, we have said nothing about the ownership structure of the firm or how this theory can be grafted into a wider macroeconomic theory. There might be potential modifications in this regard. There are two main questions that arise here. Firstly, if we suppose that firms are owned by entrepreneurs, might not the investment decision of the firm be affected by the owner's desired consumption-savings decision? Secondly, what exactly is the relationship between the firm's investment decision, its financing decision and wider financial markets? As Jack Hirshleifer (1958, 1970) later noted, we can answer these questions by reworking Fisher's full theory of investment into a "two-stage" budgeting process. Specifically, Hirshleifer noted that if we consider firms to be owned by entrepreneurs, then we must integrate Fisher's (1930) consumption-savings decision (the "first approximation") of the owner-entrepreneur with the investment decision (the "second approximation") of the firm which that entrepreneur owns. If we consider an entrepreneurial firm, i.e. a firm owned by a person, then we must endow the firm with a utility function U(.). Now, if we have the entrepreneur maximize utility with respect solely to the intertemporal investment frontier, we achieve a solution akin to point G* in Figure 2. In this case, then, it seems that the optimal investment decision of the firm is affected by owner's preferences. However, by realizing that firms have, in fact, a two-stage budgeting process by which firms first maximize present value as before (point Y*) and then borrow/lend their way to the entrepreneur's optimal solution (such as at point C* or F* in Figure 2, depending on the preferences of the firm's owner) we realize that the original point G* was not optimal. Hirshleifer refers to "investment", then, as incorporating both the "productive opportunities" implied at point Y* and the "market opportunities" offered up by points C* or F*.
The two central results of this two-stage budgeting has become known as the Fisher Separation Theorem:
We can see the first by noting that regardless of the preferences of the owner, the firm's investment decision will be such that it will position itself at Y*, thus making the maximization of present value the objective of the firm (which, of course, is equivalent to Keynes's "internal rate of return" rule of investment). The second part of the separation theorem effectively claims that the firm's financing needs are independent of the production decision. To see why more clearly, we can restate this in terms of the Neoclassical theory of "real" loanable funds set out by Fisher (1930). The demand for "loanable funds" equals desired investment plus desired borrowing of borrowers whereas the supply of "loanable funds" equals desired savings minus desired investment of savers. In Figure 2, suppose we have two entrepreneurs with identical firms, both of which start with endowment E and one invests and saves to achieve point F* while another invests and then borrows to achieve point C*. Looking carefully at Figure 2, we see that the first agent's desired investment is I1 = E1 - Y1 while his desired saving is equal to E1 - F1*. In contrast, the second agent has desired investment equal to I1 = (E1 - Y1) as well, but desires to borrow the amount (C1* - E1). Thus, the total demand for loanable funds is DLF = (E1 - Y1) + (C1* - E1) = C1* - Y1 while the total supply of loanable funds is SLF = (E1 - F1*) - (E1 - Y1) = Y1 - F1*. Now, if there is equilibrium in the market for loanable funds, then:
but by plugging in the details for these terms:
and rearranging:
Now, each agent invested E1 - Y1, thus total investment is I = 2(E1 - Y1). Simultaneously, the first agent saved (E1 - F1*) and the second agent dissaved (E1 - C1*) so total saving is S = (E1 - F1*) - (C1* - E1). Thus, the equation for loanable funds equilibrium can be rewritten simply as:
i.e. total investment equals total savings. Note the condition that for total investment to be equal to total savings, then the demand for loanable funds must equal the supply for loanable funds and this is only possible if the rate of interest is appropriately defined. If the interest rate was such that the demand for loanable funds was not equal to the supply of it, then we would also not have investment equal to savings. Thus, in Fisher's "real" theory of loanable funds, the rate of interest that equilibrates supply and demand for loanable funds will also equilibriate investment and savings. This is effectively the story in Neoclassical macroeconomic theory. [Note: our expression is slightly different from Fisher's original 1930 formulation as, instead of netting out as we have done, Fisher had the supply for loanable funds defined as savings plus disinvestment and demand for loanable funds defined as investment plus dissaving; nonetheless, the equilibrating interest rate is unchanged by whichever definition we choose.] |
All rights reserved, Gonçalo L. Fonseca