Keynesianism and the Classical System

Back

In the open Leontief system, the term we obtained  as the solution of x is as follows:

x = (I - A¢ )^-1c

This is also known as the "matrix multiplier" since it relates consumption to output in an almost Keynesian fashion. Letting D be the difference operator so that D x is a change in output and  Dc is a change in consumption, then:

D x = (I - A¢ )^-1Dc

which simply states that growth in consumption must be met by growth in output as proportioned by the inverse of the technology matrix.

This "Keynesian" result has interesting implications if we wish to think about employment and capacity utilization. If primary inputs are not producible, by definition, then one might think that they are endowed and thus limited in supply. Consequently, one may conjecture that the supply of endowed factors might constrain the level of activities x below equilibrium or, more interestingly, remain in excess. Let v be a vector of primary input supplies, v¢ = [v₁, ..., v_m], then we now have a new quantity condition that states:

B¢ x £ v

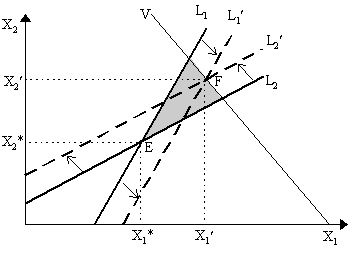
i.e. the demand for primary inputs cannot exceed their supply. In Figure 1 below we see the implications of this assumption. Allowing for inequalities x ³ Ax + c, so that we can set out the Leontief system as a linear programming problem, we obtain, in the two-sector case, the familiar L₁ and L₂ lines acting as constraints. However, the endowment restriction implies that we must add a third line, denoted V in the diagram, which places an upper bound on the possible output combinations in the economy. This arises from the equation B¢ x £ v which, in a two-sector case with one primary factor, translates into:

b₀₁X₁ + b₀₂X₂ £ v

where b₀₁ and b₀₂ are unit input coefficients of the primary factor into the two industries while v₀ is the exogenously-given factor supply. Thus, the line V has vertical intercept v₀/b₀₂ > 0, horizontal intercept v/b₀₁ > 0 and slope -b₀₁/b₀₂ < 0. Thus, only areas below V are feasible according to the primary endowment constraint. As a result, combining the restriction imposed by L₁, L₂ and V, the only feasible area remaining is the shaded area in Figure 1. All other areas have output combinations which violate one of the three conditions.

Figure 1 - Excess Capacity and Effective Demand

If we choose the output combination at point E (where output is (X₁*, X₂*)), it is obvious that L₁ and L₂ constraint are binding, but constraint V is not binding, thus there is excess capacity. As a result, if we think of v₀ as the labor supply, then the output combination (X₁*, X₂*) at E is not efficient: as V does not bind, then we have obviously left a good amount of endowed labor unemployed.

The solution to this problem is, in fact, a Keynesian one: as the horizontal and vertical intercepts of L₁ and L₂ contain C₁ and C₂ in them respectively, then if we increase consumption of good 1 (shifting L₁ to the right to L₁¢ ) and/or increase consumption of good 2 (shifting L₂ to the left to L₂¢ ), then our intersection would be at a point such as F which lies on the V constraint in Figure 1. This would be the more efficient outcome as we would eliminate the excess supply of the primary input - and we would have also increased consumption in the process. This an exogenous increase in final demands (e.g. consumption) will help us eliminate unemployment and excess capacity in the economy. There is nothing within the Leontief model which forces equilibrium to be at F - thus, being at E, is equivalent to a Keynesian unemployment equilibrium. The impetus to move to F, as John Maynard Keynes (1936) proposed, must come externally from an increase in effective demand.

Top

Back

Selected References