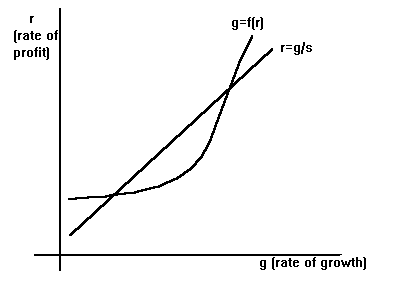Keynesian Growth: the Cambridge version

Back

The heroic entrepreneurs of Schumpeter are resurrected, only slightly less heroically, in The General Theory (1936) of J.M. Keynes. Investment, in the Keynesian system, is an independent affair contingent upon finance and the "animal spirits" of entrepreneurs.

The issue is that Keynes did not extend his theory of demand- determined equilibrium into a theory of growth. This was left for the Cambridge Keynesians to explore. The first to come up with an extension was Sir Roy F. Harrod who (concurrently with Evsey Domar) introduced the "Harrod-Domar" Model of growth (Harrod in 1939, Domar in 1946).

Recall, from Keynes, that investment is one of the determinants of aggregate demand and that aggregate demand is linked to output (or aggregate supply) via the multiplier. Abstracting from all other components, we can write that, in goods market equilibrium:

Y = (1/s)I

where Y is income, I investment, s the marginal propensity to save (and thus the multiplier is 1/s). But investment, note Harrod and Domar, increases the productive capacity of an economy and that itself should change goods market equilbrium.

For "steady state" growth, in the language of Harrod-Domar, aggregate demand must grow at the same rate as the economy's output capacity grows. Now, the investment-output ratio, I/Y, can be expressed as (I/K)(K/Y). Now, I/K is the rate of capital accumulation and K/Y is the capital-output ratio (call it "v"). Thus, the rate of capital accumulation, I/K, is the rate of capacity growth (call that "g"). Thus, for steady state it must be that I/K = (dY/dt)/Y = g (i.e. the rate of capital accumulation/capacity growth, I/K, and the real rate of output growth (dY/dt)/Y, must be at the same rate, g). Thus, plugging in our terms:

I/Y = (I/K)(K/Y) = gv

But recall our goods market equilibrium term from the multiplier, i.e. Y = (1/s)I which can be rewritten I/Y = s. Thus, the condition for full employment steady-state growth is gv = s, or simply:

g = s/v

Thus, s/v is the "warranted growth rate" of output. However, Harrod and Domar originally held s and v as constants - determined by institutional structures. This gives rise to the famous Harrodian "knife-edge": if actual growth is slower than the warranted rate, then effectively we are claiming that excess capacity is being generated, i.e. the growth of an economy's productive capacity it outstripping aggregate demand growth. This excess capacity will itself induce firms to invest less - but, then, that decline in investment will itself reduce demand growth further - and thus, in the next period, even greater excess capacity is generated.

Similarly, if actual growth is faster than the warranted growth rate, then demand growth is outstripping the economy's productive capacity. Insufficient capacity implies that entrepreneurs will try to increase capacity through investment - but that that itself is a demand increase, making the shortage even more acute. With demand always one step ahead of supply, the Harrod-Domar model guarantees that unless we have demand growth and output growth at exactly the same rate, i.e. demand is growing at the warranted rate, then the economy will either grow or collapse indefinitely.

The "knife-edge", thus, means that the steady-state growth path is unstable: the only stable growth path, the "knife-edge", is where the real growth rate is equal to s/v permanently. Any slight shock that will lead real growth to deviate from this path ensures that we will not gravitate back towards that path but will rather move further away from it.

It was up to Nicholas Kaldor (1955, 1957) to rescue this by proposing that savings are variable and would "jump" to the value necessary to bring the actual growth rate back into its warranted path. To justify this, Kaldor had to employ Classical considerations of income distribution with two classes: capitalists (who save a portion of their profits) and workers (who save from wages). Thus, letting s be the capitalists' propensity to save and s' be the workers', then total savings are:

S = sP + s'W

where P are profits and W are wages. Naturally, W + P = Y, total income is made up of profits and wages, so W = Y - P. As capitalists are assumed to save more than workers, s > s', then obviously savings are positively related to the share of profits in income, P/Y.

For goods market equilibrium, it must be that investment is equal to savings, I = S. Following the Keynesian axiom that investment is independent, then investment determines savings (or, to word it differently, aggregate demand determines aggregate supply). However, as noted profits are positively related to savings. Hence, by substitution:

I = sP + s'(Y - P)

which rearranging yields:

P/Y = [1/(s-s')](I/Y) - s'/s-s'

In other words, given the marginal propensities to save of each class, the relative size of profits in income is dependent only on the investment decision, I/Y. Naturally, the more investment, the greater the necessary slice profit takes out of income.

If we assume workers save nothing, so that s' = 0, then we quickly reach the conclusion that:

P/Y = (1/s)I/Y

where P/Y depends on I/Y. Note that this is reminiscent of Keynes' famous "widow's cruse" remark:

Or any attempt by capitalists to increase their consumption (and thus reduce savings), will merely result in increased profits - thereby generating the savings to make up for their initial decline. Or, as Kaldor (1955) reminds us, this is merely Kalecki's adage that "capitalists earn what they spend and workers spend what they earn".

What if we are not in goods market equilibrium? Suppose we have excess demand for goods so that I > S, then investment has generated a level of profits are too low for equilibrium, i.e. capitalists have not saved enough. Consequently, as pressure is placed on the goods market, prices will rise and, assuming wages are constant, real wages will fall, increasing the share of profits in income. Thus, P/Y rises, which in turn increases savings, and so on until equilibrium is re-established.

What about growth? Recall that I/Y = (I/K)(K/Y), where I/K is the rate of capital accumulation (equal to the rate of growth of productive capacity, g) and K/Y is the capital-output ratio (v). Thus, we can write I/Y = gv.

Now recall Kaldor's relationship, P/Y = (1/s)I/Y. Thus:

P/Y = gv/s

so that g = (s/v)P/Y. Recalling that v = K/Y, then this can be rewritten:

g = s(P/K)

But we should note that the ratio P/K is merely the rate of profit, r. Calling it thus, we can rewrite:

r = g/s

the rate of profit is equal to the growth rate divided by the savings rate of capitalists - which is also known as the "Cambridge rule" for growth. In a von Neumann model, recall, workers consumer everything (as here), but he also has it that capitalists save everything (so s = 1). But note that in this case, we have r = g, or "Golden Rule" growth. Thus, we immediately see the affinity between Cambridge growth models and von Neumann growth models. Morishima's (1960, 1964) extension of von Neumann models which allowed for capitalist consumption produces precisely this "Cambridge rule" for von Neumann.

Joan Robinson (1962) recommended a modification so as to understand the properties of this model better. We have not really discussed what determines investment: we simply posited a full employment relationship, i.e. I/Y = gv, so as to obtain Kaldor's steady-state. But surely, in a Keynesian world, an independent investment function should remain independent! Robinson (1962) posited a relationship I/Y = f(P/Y) or g = f(r), where investment decisions by firms were functions of (expected) profit. She argued that this was a concave function, based on Kalecki's (1937) principle of increasing risk: investment is positively related to expected profit, but at a decreasing rate - as every extra unit of investment means greater debt and thus greater risk to the firm.

However, we know from the Kaldor relationship, P/Y = (1/s)I/Y or r = g/s, that profits are themselves generated by investment. Thus, Robinson's question can be asked: when is it true that the profits generated by the investment in the Kaldor relationship will themselves generate investment decisions that, in turn, generate the original profits? Alternatively, what is there that guarantees that the profits generated by the Kaldor relationship will themselves generate the amount of investment needed to sustain them? This is a question of stability.

Robinson's (1962: p.48) diagram above of the concave Kalecki function and the linear increasing risk function is reproduced below. Assuming all is well, then we should have two equilibria where rs = g = f(r). Consider the rightmost equilibrium first. To the right of that equilibrium, Robinson posited that the economy was generating less profits than planned and thus investment plans will be shelved, inducing deaccumulation of capital and hence reducing growth. To the immediate left of it, the economy is generating more profits than planned, and thus firms will revise their expectations upwards and invest more, thereby increasing accumulation and growth. Hence, the right equilibrium is stable. A similar exercise will show that the left equilibrium is, for the same reasons, unstable.

Robinson (1962) went on to enrich her analysis by introducing labor growth and to consider the implications of including unemployment and inflation and the method of adjustment explicitly in the model. She discusses the various types of growth situations that could be encountered - Golden Rule and otherwise.

Another extension was provided by Luigi Pasinetti (1962). It is unlikely that workers do not save, as we have assumed. Originally, Kaldor (1955) proposed that workers did save out of wages, but less than capitalists - in which case, profits would be more sensitive to the investment decision than we have allowed. However, Pasinetti (1962) called this "a logical slip". If workers can save, we should conceive of two different "types" of capital falling under different ownership: "workers' capital" and "capitalists' capital". Let us call the former K' and the latter K. Thus total savings are S = sP + s'(P' + W), workers save out of both profits and wages.

It is necessary that workers be paid a rate of interest on their capital just in the same manner as capitalists receive a rate of profit on theirs. By competition and arbitrage, Pasinetti argued that the rate of profit/interest for both capitalist and workers on their capital is equalized. Or:

P/K = P'/K' = r

where P' is workers' profits. For savings, let S be capitalist savings and S' worker savings out of profits. Therefore, for steady state growth:

S/K = S'/K' = g

In the long-run, for steady-state, it must be that the rate of accumulation must be equal for both capitalists and workers, i.e.

P/S = P'/S'

otherwise, if the rate of wealth accumulation is faster for either of the classes, then there will be a change in distribution and, as a result, a change in the composition of aggregate demand. In long-run equilibrium, aggregate demand must be stable therefore this is a necessary assumption.

However, as a consequence of this assumption, we can note that:

P/sP = P'/s'(W + P')

where s and s' are the marginal propensity to save of capitalists and workers. Note again that workers also save out of wages, W, as well as profits, P', whereas capitalists only receive and save out of profits. Cross-multiplying:

s'(W + P') = sP'

Now, if investment (I) is equal to total savings which means that:

I = s'(W + P') + sP

then using our previous relationship:

I = sP' + sP = s(P + P')

Let us call total profits P* = P + P', then I = sP* or:

P* = (1/s)I

So it must be that:

r = (P*/K) = (1/s)I/K = g

i.e., for long run Golden Rule steady-state growth, only the capitalist's propensity to save needs to be considered - workers' saving propensities can be dropped by the wayside. Thus, even with worker savings, the "Cambridge rule" is iron-clad. Only capitalists' savings propensity matters. As Pasinetti notes:

But there were important assumptions in the model yet undiscussed. Pasinetti posits one of his conditions to guarantee existence to be:

s > I/Y > s'

so that profits cannot take "a null or negative share of wages" (Pasinetti, 1962). This, in essence, defines the mechanism for adjustment. If distribution can be somehow organized such that there will be a "correct" level of profits to give us the savings necessary to be in equilibrium: i.e. make I/K = s/v. The first question that must be asked here is not only whether you can calculate for a given investment level what the profit level will be but whether there will be pressures that might bring this into equilibrium. Within certain limits, Kaldor argues, variations can take place such that P/Y is a function of the change in the I/Y ratio. According to Kaldor, prices respond to relative money wage rates as a consequence of demand. Assume, for instance, that given an excess demand for goods, prices will increase but not wages. As a consequence there is a shift in distribution such that there will be an increase in the profit share. Since profits increase, this implies there will be a substantial growth in savings.

However, as J.E. Meade (1961) points out, if prices rise relative to wages, then the real wage decreases. By substitution between capital and labor, there will be a change in the capital-output ratio (v). Therefore, for Kaldorian adjustment to be applied, there is an implicit dependence on a constant capital-output ratio. However, a constant v necessarily means that we cannot be in long-run equilibrium since technique would otherwise be entirely flexible. One can perhaps regard at it as a vintage model, but here prices would have to change faster than wages. The greatest difficulty in this model, nevertheless, remains the adjustment towards the steady-state path. How do profits adjust so that one will achieve the steady-state savings rate? According to Kaldor, prices respond to relative money wage rates as a consequence of demand. Assume, for instance, that given an excess demand for goods, prices will increase but not wages. As a consequence there is a shift in distribution such that there will be an increase in the profit share. Since profits increase, this implies there will be a substantial growth in savings.

However, as J.E. Meade (1961, 1963, 1966) points out, if prices rise relative to wages, then the real wage decreases. By substitution between capital and labor, there will be a change in the capital-output ratio (v). Therefore, for Kaldorian adjustment to be applied, there is an implicit dependence on a constant capital-output ratio. However, a constant K/Y necessarily means that we cannot be in long-run equilibrium since technique would otherwise be entirely flexible.

But a more general criticism can be made. We can note that given a stock of capital, labor and output, if prices move faster than wages, then profits will increase whereas if wages move faster than prices, then profits will fall - without changing techniques. The variety of consequences of this has led several economists, such as Meade (1961) and, later, Nell (1982), to argue that at least for a long-run model, Kaldor's theory has a rather poor price-adjustment mechanism. "Mr. Kaldor's theory of distribution is more appropriate for the explanation of short-run inflation than of long-run growth." (Meade, 1961: x).

Top

Selected References

Back