|
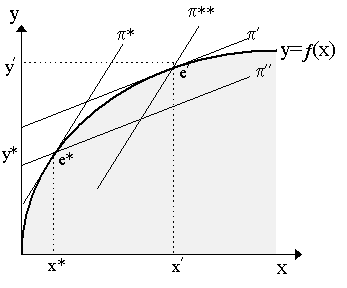
Contents (A) Profit-Maximization The profit-maximization exercise is not easily illustrated with isoquants. A better illustration is depicted in Figure 9.1, where we have production function y = ¦ (x). We should interpret this as a one-output, one-input production function, thus x is the only input and the concavity of the production function depicts decreasing returns to scale. [Note: an alternative interpretation of Figure 9.1 would be to consider y = Y/L and x = K/L, so that y = ¦ (x) depicted in Figure 9.1 would be an intensive production function, consistent with constant returns to scale. However, note that this maneouvre would not restore determinacy: in this case, we would not be determining the profit-maximizing level of output and factor inputs, but rather profit-maximizing output-labor ratios and capital-labor ratios, which is entirely consistent with indeterminacy in levels. For determinacy of levels, we must assume diminishing returns to scale, there is no way around it.] Returning to the problem at hand, note that at any output-input combination, (y, x), profit is defined as p = py - wx, where w is the only factor price and p is the output price, both of which are given. This profit equation defines a function in y-x space of the following linear form:
known as an isoprofit curve. The vertical intercept of the isoprofit curve is p /p and the slope is (w/p). This is depicted in Figure 9.1 as an upward-sloping straight line. Any combination of (y, x) on a particular isoprofit curve has the same profit, p . Thus, a given set of prices (p, w) defines a whole series of parallel isoprofit curves. In Figure 9.1, we can see that isoprofit curves p * and p ** have the same slope (and thus are generated by the same prices, (w/p)*). However, since p * lies to the northwest of p **, it has a higher vertical intercept which implies that p * represents higher profits than p **. Notice that a different set of prices will yield a different set of parallel isoprofit curves (e.g. p ¢ and p ¢ ¢ in Figure 9.1, with p ¢ representing higher profits than p ¢ ¢ ).
In this simple one-output, one-input case, the profit-maximizing solution is easy to describe. Suppose output prices and factor prices are (w/p)* so that we generate the isoprofit curves p *, p **. Compare now two points in Figure 9.1, e* = (y*, x*) and e¢ = (y¢ , x¢ ). At e*, profits are p * while at e¢ , profits are p **, thus obviously output-input combination e* has greater profits than output combination e¢ , thus a profit-maximizing producer facing prices (w/p)* would decide against e¢ and for e*. Notice, indeed, that the isoprofit curve p * is tangent to the production function at e*, thus of all the isoprofit curves generated by factor prices (w/p)*, p * is the most northwesterly of them, i.e. the highest profits. Thus, e* is the profit-maximizing output-input combination. This tangency result implies that the slope of the isoprofit contour p * is equal to the slope of the production function, dy/dx, i.e.
But dy/dx = ¦x, thus this merely states that p¦x = w, precisely the first order condition we obtain from the profit-maximization problem. Thus, e* is definitely profit-maximizing at these prices. In contrast, at e¢ , the slope of the isoprofit curve p ** is greater than that of the production function, implying that w > p¦x, i.e. marginal cost of the factor is greater than the marginal value product. This clearly violates the first order conditions. Suppose now factor prices change so that we obtain isoprofit curves p ¢ and p ¢ ¢ . As these curves are flatter than the previous ones, this implies that (w/p)¢ < (w/p)*, i.e. the factor price has declined and/or the output price increased. Notice that now e* is no longer profit maximizing. Specifically, the isoprofit curve at e* is now p ¢ ¢ , which is flatter than the slope of the production function at e*, i.e. dy/dx > w/p, thus the marginal value product is greater than the factor return, consequently it is profitable to increase factor employment and output. Combination e¢ , the tangency of the highest isoprofit curve at the new prices, p ¢ , with the production function, is now the profit-maximizing combination. Notice that y¢ > y* and x¢ > x*, thus we are producing at a greater scale at the new prices than we were at the old prices. In sum, we have detected a few things. Firstly, the strict concavity of the production function enables us to define unique profit-maximizing output-input combinations for any particular set of output-input prices, w/p. Secondly, the profit-maximizing combination will be at the tangency of the isoprofit curve and the production function. Thirdly, a rise in the output price and/or a fall in the factor price will increase the profit-maximizing level of output. Of course, all this is for the one-output, one-input production function in Figure 9.1. If we had more inputs, we would not be able to draw it in a two-dimensional diagram but the lesson is basically the same, only now we would have to be careful about the relative prices of the factors. Specifically, if we had our canonical case, Y = ¦ (K, L), it is not clear what a change in the factor price ratio r/w would be on output. We know, for certain, by our earlier first order conditions, that if r/w rose, then, the profit-maximizing producer would employ more labor relative to capital, but it is not clear, at least at this stage, whether the scale of production would be increased or decreased as well. In our cost-minimization exercise, we were able to derive a cost function C(w, y) and a compensated factor demand function x = x(w, y). There are analogues in the profit-maximization case. The first is the profit function, which is defined as :
where the terms follow their traditional definitions (w and x are vector of factor prices and factor demands respectively). Notice that output price (p) and factor prices (w) the only parameters entering into profit-function. The profit function maps particular factor prices to the maximum profit levels achievable at those output prices and factor prices. Thus, in terms of Figure 9.1, prices (p, w)* would be mapped to profit level p * (not p **) while prices (p, w)¢ would be mapped to profit level p ¢ (not p ¢ ¢ ). The profit function is due in large part to the pioneering work of Harold Hotelling (1932). The following are its standard properties:
Property (1) is straightforward: a producer will not tolerate negative profits. If he is making negative profits, he can always stop all production and be better off. Of course, this is not completely realistic: producers may be willing to make temporary losses, at least for a little while. But, as that is temporary, one might as well simply restrict profits to be non-negative. Property (2) ought to be also clear. If output price increases and factor prices remain unchanged, then the maximum profits increase. To see why, suppose p¢ ³ p. At p, (y, x) is chosen as profit-maximizing level of output and inputs, thus p (p, w) = py - wx. If output price increases to p¢ but the producer decides to remain at (y, x), then immediately we see that profits become p¢ y - wx ³ py - wx, so profits increase by the amount (p¢ -p)y. Thus, when deciding upon his profit-maximizing combination (y¢ , x¢ ), he will not move to a situation which yields less profits than that. In short, profits at the new position, p (p¢ , w), will not fall. Property (3) is similar to (2). It simply states that if a factor price increases and all other prices are the same, then profits will fall. To see why, let w¢ ³ w. Suppose at w, x yielded maximum profits, i.e. p (p, w) = p¦ (x) - wx. Suppose that at w¢ , x¢ is yields maximum profits, i.e. p (p, w¢ ) = p¦ (x¢ ) - w¢ x¢ . Now, at prices w, x¢ might have been available but was not chosen, thus implying that p¦ (x) - wx ³ p¦ (x¢ ) - wx¢ , otherwise x would not have been profit-maximizing. But as w¢ ³ w, then w¢ x¢ ³ wx¢ or subtracting both from p¦ (x¢ ), p¦ (x¢ ) - w¢ x¢ £ p¦ (x¢ ) - wx¢ . Thus combining inequalities p¦ (x¢ ) - w¢ x¢ £ p¦ (x) - wx, or simply p (p, w¢ ) £ p (p, w). Thus inequality (3). Property (4), the convexity of the profit function, can be stated as follows:
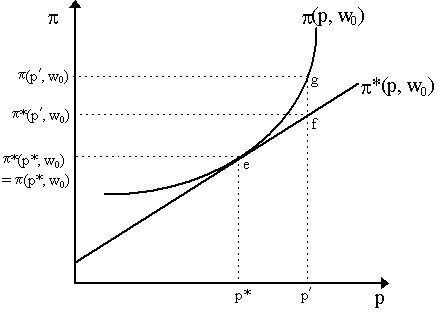
The formal proof is elementary and as we do this elsewhere, we shall only give the intuitional result via Figure 9.2 where we plot profits against output price, p, thus we are holding factor prices fixed at w0. Consider a particular output-input bundle (y*, x*). At price combination (p,w0), profit for this particular is defined as p *(p, w0) = py* - w0x*. Keeping other factor prices constant at w0 and varying only p, we see that profits from this bundle are linearly related to output price p. This is shown in Figure 9.2 by the linear function p *(p, w0). Suppose that there is a particular price level, p* where the bundle (y*, x*) happens to be profit-maximizing. This is shown in Figure 9.2 as point e.
Suppose now we increase prices from p* to p¢ and the producer must make a new profit-maximizing output-input choice (y¢ , x¢ ). However, we have already shown in property (2) that if output price increases and factor prices remain unchanged, then the producer not choose a bundle which yields less profits. In other words, the bundle (y¢ , x¢ ) chosen at higher price p¢ cannot yield less profits than the old bundle (y*, x*), i.e. p (p¢ , w0) = p¢ y¢ - w0x¢ ³ p¢ y* - w0x* = p *(p¢ , w0), shown by the fact that point g on the profit function p (p, w0) lies above point f on the linear function p*(p, w0) . Thus, in principle, to the right of p*, the profit function p (p, w0) is everywhere above p *(p, w0). A similar reasoning in reverse establishes that everywhere below p*, p (p, w0) ³ p *(p, w0). Thus the convexity of the profit function in Figure 9.2. A reverse convexity will be obtained if we plot p (p, w) against a particular factor price, wi. One can quickly notice that, if differentiable, the convexity of the profit function implies that the Hessian matrix:
is symmetric and positive semi-definite. Property (5), continuity, is omitted here (a formal proof is contained elsewhere). Property (6), the homogeneity of degree one in prices is easy. Note that p (p, w) = maxy, x [py - wx] by definition. Consequently, p (l p, l w) = max y, x [l py - l wx], thus factoring l outside the max operator, p (l p, l w) = l max y, x [py - wx] = l p (p, w), thus homogeneity. Property (7), Hotelling's Lemma (from Hotelling (1932)) is as famous as Shephard's Lemma and is analogous. Namely, if profit functions are differentiable at p and w, then Hotelling's lemma claims that:
and:
In other words, differentiating the profit function with respect to output price yields output quantity, while differentiating it with respect to price of a particular factor yields (the negative of) the corresponding factor quantity. Notice that y(p, w) and xi(p, w) are, respectively, the profit-maximizing output level - a.k.a. the supply function - and profit-maximizing demand for factors - the (uncompensated) factor demand function. Thus, Hotelling's Lemma enables us to obtain supply functions and factor demand functions merely by the derivative of the profit function. (notice also: if the profit function is differentiable, then output supply and factor demand are uniquely defined; conversely, if output supply and factor demand are unique, then p (p, w) is differentiable). The proof of Hotelling's Lemma is straightforward algebra. Suppose that at prices (p, w), the profit-maximizing output-input combination is (y, x), where y = y(p, w) and x = x(p, w) by definition. Now, output is produced from factors, thus we can also write y = ¦ (x(p, w)), i.e. the optimal output level is a function of the optimal input level. Plugging the optimized values into the definition of profit:
Now, differentiating with respect to p, we obtain:
Now, ¶¦ /¶xi is merely ¦i, the marginal product of factor i and, recall, ¦(x(p, w)) = y(p, w). Thus, rearranging the expression:
but notice that the term in the brackets, p¦ i - wi = 0 by the first order conditions of profit-maximization. Consequently this reduces to:
which is Hotelling's lemma with respect to output prices. For factor prices, differentiate the optimized profit function with respect to wi:
Where, again by the same reasoning via first order conditions for profit-maximization, reduces to:
which is Hotelling's Lemma with respect to factor prices. (C) Output Supply and Factor Demand Functions From the cost function, we obtained a compensated factor demand function xi(p, y) as the optimized arguments. Similarly, from the profit function, we derive the output supply function y(p, w) and the (uncompensated or conventional) factor demand function xi(p, w). What are the properties of these supply and factor demand functions? Analogously to the cost-minimization case, we can squeeze Hotelling's lemma for all its worth to obtain the following straightforward relationships:
(1) and (2) are straightforward applications of Hotelling's lemma, i.e. for (1) ¶ y/¶ p = ¶2p(p, w)/¶ p2 ³ 0 and ¶ xi/¶ wi = -¶2p(p, w)/¶ wi2 £ 0 by convexity of the profit function. (3) and (4) are similar applications, i.e. ¶ xi/¶ wj = -¶¶2p(p, w)/¶wi ¶wj = -¶2p(p, w)/¶ wj¶wi = ¶xj(p, w)/¶wi and ¶ y/¶ wi = ¶2p(p, w)/¶ p¶ wi = ¶2p(p, w)/¶ wi¶ p = -¶ xi(p, w)/¶ p. Now, recall from cost-minimization we obtained the compensated factor demand function xi(p, y) while from profit-maximization we had an uncompensated demand function xi(p, w). These are obviously different functions, but is there any relationship? Indeed, there is. Recall that the profit function can be stated as:
Now, let y* = y(p, w) be the profit-maximizing supply that solves this. Consequently, plugging in:
which follows from the fact that y* is already optimized, so all that remains is the minimization of wx. However, notice that this can be rewritten as:
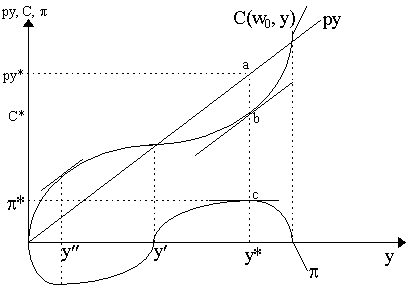
where C(w, y*) is the familiar cost function with the given y*. In other words, cost-minimization yields the same result as profit-maximization when the given output level is the profit-maximizing output, y*. This is illustrated in Figure 9.3, where we have plotted the familiar cost curve C(w0, y) plotted against ouput with constant factor prices w0, together with the revenue curve py. Along the horizontal axis, we have plotted profits, which correspond to the vertical distance between py and C(w0, y). Obviously, a profit-maximizing producer would produce at output level y*, where the vertical distance between the curves is positive and large (i.e. between a and b in Figure 9.3). Notice that we only obtain a well-defined maximum profits p * due to the convexity of the cost curve (and concavity of profits) above the inflection point y¢ , which, as we know, reflects increasing costs/diminishing returns to scale.
Returning to our profit function p (p, w) = py* - C(w, y*), notice that differentiating with respect to wi, we obtain:
By Hotelling's lemma the term on the left is x(p, w) whereas by Shephard's lemma, the term on the right is merely x(w, y*), thus:
in other words, the uncompensated and compensated factor demands are the same if the compensated factor demand is obtained from the cost-minimization at the profit-maximizing output level, y*. This relationship should be self-evident geometrically. The magic of this relationship is that we can use it to decompose the change in uncompensated factor demand for factor xi with respect to a rise in the factor price wj. In other words, we wish to express its slope ¶ xi(p, w)/¶ wj. To do this, take the total derivative of the uncompensated-compensated demand equality with respect to wj:
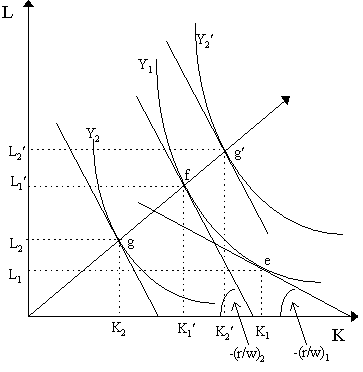
This states that if the price of factor i rises, then it feeds into a change in factor demands x(p, w) via two main channels - the substitution effect, represented by the term ¶ x(w, y*)/¶ wj on the left, and the output effect, represented by the term on the right, (¶ xi(w, y*)/¶ y)·(¶ y*/¶ wj). We ought to be able to disentangle the meaning somewhat by considering Figure 9.4, where we have our canonical production case Y = ¦ (K, L). At factor prices (r/w)1, suppose the producer choose output level Y1 and factor combination (K1, L1), represented by point e. Suppose that we now raise the rental rate on capital, r or decrease w. What happens to the demand for capital and labor? The substitution effect, as we gather from the expression ¶ x(w, y*)/¶ wj, establishes the effect on compensated demand from a rise in prices. In other words, we change the relative prices and run the cost-minimization exercise again on the same old isoquant. As we see immediately in Figure 9.4, holding output constant at Y1, a rise in factor price ratio to r2/w2 will lead, by cost-minimization, to point f on the isoquant Y1. Thus, by the substitution effect, a rise in r or fall in w leads necessarily to a fall in the demand for capital from K1 to K1¢ and a rise in demand from labor from L1 to L1¢ .
However, there is also the ugly term on the right, the output effect. This is harder to disentangle as it will be different depending on whether the increase in r/w arises from a rise in r or a fall in w.. The basic idea is the following: if factor price wj rises (all other unchanged), then marginal costs rise; if marginal costs rise, in principle, we would like to see output fall. If output falls, then the demand for both factors will decline (if both factors are normal). This is represented by a move down the output expansion path towards the origin. In Figure 9.4, r/w rose and the substitution effect took us from e to f, but whether we move to a higher or lower isoquant depends upon whether r/w rose because of a rise in r (in which case we move to point g on the lower isoquant Y2) or because of a fall in w (in which case we move to point g¢ on the higher isoquant Y2¢ ). The reason for this is, once again, because a rise in r will raise marginal cost and thus decrease output, whereas a fall in w will reduce marginal cost and thus increase output. The net effect can be ambiguous, but as we have drawn it in Figure 9.4, whether we end up at g or at g¢ , labor demand rises (from L1 to L2 or L2¢ , depending on which way the output effect works) and capital demand falls (from K1 to K2 or K2¢ ). This is what one would normally expect, but it is by no means guaranteed. As we can envision, K and L are net substitutes (in terms of compensated demand functions, ¶ L/¶ r ³ 0 and ¶ K/¶ w ³ 0) but may be gross complements if the output effect is adverse and strong enough, i.e. it may be that in the end ¶ L/¶ r £ 0 or ¶ K/¶ w £ 0. As it is written, the output effect is a bit hard to decipher and not very intuitive. In the form it is in, (¶ xi(w, y*)/¶ y)·(¶ y*/¶ wj), it simple states the change that would occur in the cost-minimizing demand for good i if we increased the profit-maximizing output level in response to a change in the price of factor j. There are numerous alternative ways of expressing this and how we proceed is actually a matter of taste. The most intuitive way is perhaps the following. Let us detail the ¶ y*/¶ wj component of the output effect. By the reciprocity relationship (4), we have it that ¶ y*/¶ wj = -¶ xj(p, w)/¶ p. However, this last term is no less obscure. To understand it, recognize that there is a uncompensated-compensated equality for factor j, i.e. xj(p, w) = xj(w, y). Thus, differentiating this with respect to p, we obtain:
As ¶ y*/¶ p ³ 0 by the non-decreasing property of the supply function, then this effectively states that the rise in output in response to a change in a factor price (¶ y*/¶ wj = -¶ xj(p, w)/¶ p) will move in the opposite direction in which cost-minimizing demand for factor xj adjusts in response to a change in output. A further interpretation is in order. Remember from our cost function that ¶ xj(w, y*)/¶ y = ¶ 2C/¶ wj¶ y = ¶ (¶ C/¶ y)/¶ wj. Thus, the expression ¶ xj(w, y*) /¶ y captures the effect of a rise in factor price wj on the marginal cost of output. For a normal factor, we would expect ¶ xj(w, y*)/¶ y ³ 0, which implies that ¶ y*/¶ wj £ 0, which is effectively what we have in Figure 9.4 by the inward shift in output fom Y1 to Y2. In contrast, for an inferior factor ¶ xj(w, y*)/¶ y ³ 0, so it must be that ¶ y*/¶ wj ³ 0, which is the outward shift in output from Y1 to Y2¢ . Thus, putting this all together, our decomposition can be rewritten completely as:
The intuition for the output effect can be made a bit clearer now. Effectively, a rise in the factor price wj raises marginal cost of output (¶ C/¶ y); this will lead to a response in output level according to the supply function relationship (¶ y*/¶ p). This change in output then feeds into a change in the demand for the factor xi, captured here by ¶ xi(w, y*)/¶ y. The sign of the output effect thus depends on the signs of its component terms: if xj is a normal factor, then ¶ (¶ C/¶ y))/¶ wj ³ 0; we know that ¶ y*/¶ p ³ 0 from before; finally, if xi is a normal factor, then ¶ xi(w, y*)/¶ y ³ 0. Thus, in total, the output effect says that a rise in wj will lead to a decline in the demand for factor i, exactly as we expected for normal factors. If the notation is confusing, consider how it looks for our canonical case when we try to figure the impact of the rise in the rental rate of capital on the demand for labor:
where MC is marginal cost, Y is output and p is price level. The interepretation can be read again with this more familiar notation in mind. The following are alternative decompositions of the uncompensated demand function. Originally we have:
Applying reciprocity ¶ xj(p, w)/¶ p = -¶ y*/¶ wj, we get:
Applying ¶ xi(w, y*)/¶ y = -(¶ y*/¶ wi)/(¶ y*/¶ p) from the differentiation of the uncompensated-compensated equality with respect to p:
Applying reciprocity again:
This last is particularly useful when we analyze the own-effect, i.e. the change in demand for a factor by a change in its own price. In this case we have:
Notice that as (¶ xi(p, w)/¶ p)2 ³ 0 necessarily and ¶ y*/¶ p ³ 0 from the properties of supply. This implies that ¶ xi(p, w)/¶ wi £ ¶ xi(w, y*)/¶ wi, i.e. the uncompensated factor demand function xi(p, w) is steeper than the compensated demand function, xi(p, y). This is obvious in Figure 9.4: a rise in r (keeping w constant) will result in a compensated move from e to f and an uncompensated move from e to g. Thus, the fall in uncompensated demand for capital (from K1 to K2) will be greater than the fall in compensated demand (from K1 to K1¢ ) One can express the decomposition in elasticity form as follows. Let us take the following simplest decomposition of demand:
multiplying through by wj/xi(p, w):
The term on the left side of the equation is, of course, e ij(p, w), i.e.
the elasticity of uncompensated demand for factor xi with respect to factor price wj. Then, recongnizing that xi(p, w) = xi(p, y*), then the term that was the substitution effect can be rendered as:
i.e. the elasticity of compensated demand with respect to factor price wj. All that remains is the output effect. Multiplying through by 1 = y*/y*, we obtain:
Defining the elasticity of factor i demand with respect to output as e iy = ¶ ln xi(p, w)/¶ ln y and the elasticity of output with respect to factor price j as e yj = ¶ ln y(p, w)/¶ ln wj, then this entire term reduces to:
This is not necessarily a very informative expression. The best thing to do is to re-express it as follows. Define the elasticity of supply as e yp = ¶ ln y(p, w)/¶ ln p. Thus, multiplying the last expression by 1 = e yp/e yp:
Now, we with to disentangle e yj/e yp. As we know form reciprocity and other relationships:
Thus:
Thus, dividing through by e yp = (¶ y*/¶ p)·(p/y*):
so cancelling:
But recall by the definition of the cost function that ¶ xj(p, y*)/¶ y = ¶ (¶ C/¶ y)/¶ wj), thus we can rewrite this as:
If we assume price equals marginal cost (p = ¶ C/¶ y, as it would be in perfect competition), this term has an interesting interpretation, namely e yj/e yp is merely the elasticity of marginal cost with respect to factor price wj. Let us rewrite then e mj = -e yj/e yp, so our elasticity decomposition becomes:
which follows our previous intuition. Specifically, this states that the responsiveness of factor demand xi with respect to factor price wj depends on the elasticity of the uncompensated demand (e ij), the responsiveness of factor demand xi with respect to output (e iy), the responsiveness of output with respect to price (e yp, the elasticity of supply) and, finally, the responsiveness of marginal cost to factor price wj (e mj). This fits our intuition nicely. We can do even better if we assume constant returns to scale and output-market clearing. This, of course, is an illegitimate move in this context, but nonetheless useful as it brings it closer to Alfred Marshall's (1890: p.319-20) speculations on derived demand. Specifically, Marshall noted that when the price of a factor rises, the degree to which other things are affected depend upon the degree of substitutability between factors, the elasticity of demand for output, the share of that factor's payments in total costs and the elasticity of supply of other factors. With some tricky adjustments, all these elements, (except the last - as we assume the prices of other factors to be fixed), can be read into our decomposition of factor demand. To see this, note that e mj = (¶ MC/¶ wj)·(wj/p). So, assuming perfect competition so p = MC, we can thus think of e mj = (¶ p/¶ wj)·(wj/p). Under constant returns to scale, we know that by Euler's Theorem , y = å i=1m ¦ ixi. Consequently, multiplying through by p and recalling that p¦ i = wi by the first order conditions for profit maximization, we obtain py = å i=1m wixi or, dividing through by y, yields p = å i=1m wixi/y. Thus:
therefore:
But, as we know, under constant returns to scale, py = å i=1m wixi, i.e. total costs. Thus e mi expresses the share of paayments to factor j in total costs, i.e. e mj = sj. Thus, we can rewrite our decomposition as:
Now, we can also reduce the e iy into more a simpler term. Recognize that when moving from point f to points g or g¢ in Figure 9.4, we are moving along a ray, i.e. there are fixed factor proportions in the output effect. As a consequence, a proportional change in any factor will be equal to a proportional change in output, i.e. ¶ xi/xi = ¶ y/y, i.e. e iy = (¶ xi/¶ y) = 1. This simplifies things considerably, so our decomposition becomes simply:
Now, e yp is the elasticity of output with respect to output price. As we have assumed constant returns to scale, the supply curve is flat, so e yp no longer seems to make sense. However, assuming market clearing, so yd = y(p, w), we can reinterpet eyp as capturing the price elasticity of demand for that output. In more conventional terms, e yp = h (where h = - ¶ ln yd/¶ ln p, thus downward-sloping demand implies h > 0). As a result:
Finally, recall from our earlier section that e ij, the elasticity of compensated demand of factor i with respect to the price of factor j, can be expressed as e ij = sjs ijA where sj is the share of factor j in total costs and s ijA is the Allen elasticity of substitution. Consequently, we can express the entire decomposition as:
which is precisely the form we find it in R.G.D. Allen (1938: p.508). This representation is as useful and as intuitive as possible. We can notice that the elasticity of demand for a factor i with respect to factor price j depends on the elasticity of demand for the output (h), the elasticity of substitution between the two factors involved and the share of the factor in total costs (sj) - three of Alfred Marshall's four elements. The signs for the output effect follow our intuition. If sj = 0 so that factor j is not used in production, we would not expect a rise in wj to increase demand for that factor (and it is impossible to decrease demand further). If the share of factor j is very high, then a rise in factor price wj will affect marginal cost of output tremendously (recall, e mj = sj), thus the greater the size of the output effect. Now, a rise in marginal cost, in our competitive system, feeds immediately into a rise in output price. The more sensitive demand is to output price (the higher h ), the greater the necessary fall in output will be. As demand for factor i varies proportionally with output, then the greater the necessary collapse in demand for factor xi. Thus, a high h implies a strong output effect. The substitution effect also makes sense. The Allen elasticity s ijA reflects the "curvature" of the isoquant, thus the more curved it is, the less substitutable (and more complementary, if s ijA < 0) the factors in question are. Consequently, a high s ijA implies high substitutability: thus demand for factor i would rise more in response to a rise in the price of the competing factor wj the greater s ijA is. Finally, the greater the share of factor j in costs, i.e. the greater sj, the more it pays to move away from it and towards factor i when its price rises. Finally, let us turn to substitution and complementarity. In general, we say that two different factors i and j are net substitutes if ¶ xi(w, y*)/¶ wj ³ 0 and net complements if ¶ xi(w, y*)/¶ wj ³ 0. We say they are gross substitutes if ¶ xi(p, w) /¶ wj ³ 0 where i ¹ j and gross complements if ¶ xi(p, w) /¶ wj £ 0. Notice that "net" refers to compensated demand (and thus confines itself to the substitution effect), while "gross" refers to uncompensated demand (and thus includes the output effect). It is obviously possible that net substitute goods become gross complements if the output effect is both adverse (i.e. moves in the wrong direction) and large enough. In other words, we need it that (¶ xi(w, y*)/¶ y)·(¶ y*/¶ wj) £ 0 and large. For this to be true, then one of two possibilities arise: (1) xi must be inferior (i.e. demand for it falls with a rise in output) and output rises in response to a rise in wj; (2) xi is normal (i.e. demand rises with rise in output) and output falls in response to a rise in wj. However, notice by the reciprocity condition (4) that ¶ y*/¶ wj = -¶ xj(p, w)/¶ p = -(¶ xj(w, y*)/¶ y)·(¶ y*/¶ p). As ¶ y*/¶ p ³ 0, then ¶ y*/¶ wj ³ 0 if and only if (¶ xj(w, y*)/¶ y) £ 0, i.e. good j is inferior. Thus, we can change the condition to (1) both goods must be normal; (2) both goods must be inferior. Thus, if we have two net substitutes, one inferior and one normal, we will not obtain gross complementarity.
|
All rights reserved, Gonçalo L. Fonseca