|
Notation Options are one of the more interesting securities to which arbitrage reasoning can be applied. (European) options, recall, are assets who derive their value from an underlying security, thus they have a return structure ro = [max(0, r1 - c), max(0, r2 - c), .., max(0, rS-c)] where r1, r2, .., rS are the returns on the underlying security and c is the "strike" price. The strike price is the asset price at which the owner of the option is entitled to buy (if a call option) or sell (if a put option) a unit of an underlying security if he decides to "exercise" it. One of the more interesting results, as stressed by Stephen Ross (1976), is that we can use options to "complete" incomplete markets: specifically, we can construct options to span a space when there are an insufficient number of fundamental assets. To see this, suppose we have three states S = (1, 2, 3) but only one asset f which pays returns rf = (1, 2, 3). Clearly, markets are incomplete as rank(V) = 1 < 3 = S. However, all we have to subsequently do is set up two options with different strike prices in order to be able to span the set of states. To see this, suppose we construct an option (call it p) with strike price 1.5. In this case, the returns on the option p are rp = [max(0, 1 - 1.5), max(0, 2-1.5), max(0, 3-1.5)] which turns out to be rp = (-0.5, 0.5, 2.5) which is linearly independent from rf as there is no l such that l rf = rp. Similarly, another option (call it q) with strike price 1.5 will have return structure rq = [max(0, 1 - 2.5), max(0, 2-2.5), max(0, 3-2.5)] or rp = (-1.5, -0.5, 0.5) which, again, is linearly independent of rf as well as rp. Thus, we now have three securities (two options and an underlying security) with linearly independent returns - thus, we can now completely span the set of state returns. In principle, as Ross (1976) indicates, in any situation of incomplete markets, options can be constructed on existing assets to restore completeness. The only caveat is that if the underlying asset pays the same returns in any two states, then completion via options will not be possible. The question that emerges immediately is how options are priced. The celebrated theorem of Fisher Black and Myron Scholes (1973) effectively makes use of the reasoning we have already employed here - indeed, it was one of the first papers to exploit the concept of arbitrage and the linear pricing rule. The basic idea is to "replicate" the returns on the option by constructing a portfolio of fundamental assets. By consequent arbitrage reasoning, then, the value of the option is equal to the value of this portfolio. Consider the following simple example, which follows the "binomial" approach of Cox, Ross and Rubinstein (1979). Suppose we have two states (S = (1, 2)) and two fundamental assets (a riskless bond and a risky stock) and suppose that we have a call option on the stock. The bond has return structure rb = (1, 1) while the stock has return structure re = (3, 0.5). Suppose the call price of the option on the stock is c = 1, thus it has return structure ro = [max(3 - c, 0), (0.5 - c, 0)] = [2, 0] (notice that in this case, the option is not exercised in the second state). Now, if were to construct a replicating portfolio of bonds and stocks then we would need to find portfolio purchases, ab for bonds and ae for stocks, so that in each state, the returns to this portfolio would be the same as that of the option Specifically, we need it that for the first state:
and for the second state:
Thus, the portfolio returns replicate the option returns. We have two equations and two unknowns (ab, ac). Solving simultaneously we can see that the result will be ab = 0.4 and ae = -0.8 so the required portfolio will have 0.4 units of a bond and -0.8 units of a stock (thus purchasing bonds, short-selling stocks). By the arbitrage reasoning of the linear pricing rule, the value of this portfolio will be the same as the value of the option, thus qo = 0.4qb - 0.8qs where, if we know qb and qs, we can compute this. Notice that as we know that qf = å sÎ S msrfs by the fundamental theorem, then in this case:
Normalizing qb = 1, then m 1 = 1 - m 2 from the first equation; plugging into the second and solving, we obtain qe = 3 - 2.5m 2. Thus, the value of the option will be:
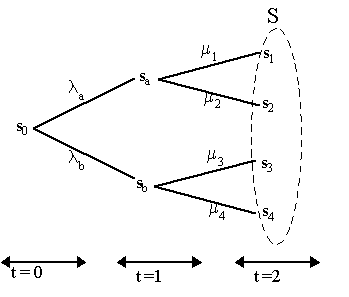
Thus, all we have to know is m 2 and we're home. For more details on option pricing, see Cox, Ross and Rubinstein (1979), Cox and Rubinstein (1985) and the standard texts noted earlier. The idea of the "completion" of asset markets by options has an analogue in multiperiod models with long-term securities - what has been called "dynamic completion". The basic idea is that we can use far fewer securities to span the state returns space than might seem necessary at first glance. Recall that in a multi-period model, we can lay out the resulting succession of states over time via a "tree" with nodes and a final set of end-states, S. An example is shown in Figure 6, where we have three time periods t = (1, 2, 3). The final set of states (at t = 3) is S = (s1, s2, s3, s4). The first node (s0) represents the initial state at t = 0 and the pair of nodes (sa, sb) at t = 1 are intermediate states. As noted elsewhere, we can achieve a Radner equilibrium with long-term assets that pay in the final set of states, i.e. "long-term" or "long-lived" securities. As we have S final states, we would suspect that we might need S long-term assets for "complete" markets. However, as initially suggested by David Kreps (1982) and generalized by Darrell Duffie and Chi-Fu Huang (1985), we could actually use less than S long-term assets to span the state-returns space, as long as we are allowed to trade them repeatedly. To see this, let us suppose we have a situation as in Figure 6. Let us have two long-term assets ¦ and g, which pay off in the final states only. Let the possible returns in time t = 3 be rf = [1, 0, 1, 0] and rg = [1, 1, 1, 1] so asset f pays a positive return in final states s1 and s3 and 0 elsewhere, while g pays a sure return of 1 in all final states. Then our returns matrix is:
where, note, rank(V) = 2 < S = 4, so it seems as if we have incomplete markets. However, as we shall see, this imposes no difficulty. Now, asset markets are open at the initial and intermediate nodes, thus we have three sets of asset prices to consider: q0 = (qf0, qg0) at initial state s0, qa = (qfa, qga) at intermediate node sa and qb = (qfb, qgb) at intermediate node sb.
We wish to determine the entire set of asset prices, qf0, qg0, qfa, qga, qfb, qgb. By the fundamental theorem of asset pricing, we know that the price of an asset is the sum of its returns weighted by the state prices, m s. However, with the tree-structure we have in Figure 6, we need only consider them a step at a time. For instance, suppose we are in the intermediate node sa where, note, the final states s1 and s2 are the only future states achievable from there. Now, as we have two assets, then we wish to consider only qfa, qga at node sa. Consequently, as asset markets at that node must be in equilibrium, then the fundamental theorem applies to these asset prices, but we only need to consider the multipliers m 1, m 2 associated with s1, s2. Thus, by the fundamental theorem:
so as rf = [1, 0, 1, 0] and rg = [1, 1, 1, 1], then:
Similarly, at intermediate node sb, where only s3 and s4 are possible consequences in the final period, we have from the fundamental theorem applied at sb:
where m 3, m 4 are the state prices for final states s3, s4. Again, given our return structures:
Consider now asset prices in the initial state, s0. Now, we do not have returns for assets f and g in the intermediate states as these are long-lived assets, but we do have their asset prices. Thus, we can think of the possible "returns" at t = 1 to purchasing a unit of a long-lived asset f at t = 0 as its sale prices in the two possible intermediate states, i.e. qfa, qfb. Thus, letting la and lb be the multipliers associated with the intermediate states sa, sb, then applying the fundamental theorem to the asset prices of asset f and g at the initial state, we have:
But recall that we have expressions for qfa, qfb, qga, qgb already. Thus this becomes by substitution:
which would then constitute the initial asset prices for the long-lived assets f and g. Now, recall that we have a separate budget constraint at each node. Thus, letting akh be the set of assets purchased in any particular node k (i.e. k = 0 , a, b), then the hth agent who derives utility from consumption in every node faces the following Radner optimization problem:
thus we have nine budget constraints, one for each node. Notation is standard: pk are the spot prices, xkh are commodity bundles, ekh are the endowments, qk are asset prices and akh are assets purchased at any node k Î (0, a, b, 1, 2, 3, 4). Vs is the sth row of V = [rf¢ , rg¢ ]. Heuristically, we can see that we can collapse these multiple budget constraints into a single Arrow-Debreu constraint at t = 0. Namely, assuming an interior solution (and thus equalities), we can express the final two budget constraints for aah and abh respectively. We can then plug these terms into the intermediate constraints and then re-express these for a0h which we then plug into the initial constraint. To see this more clearly, let us note it explicitly for our particular example where rf = [1, 0, 1, 0] and rg = [1, 1, 1, 1]. The portfolio purchased at node a is aah = [afah, agah]¢ and that purchased at node b is abh = [afbh, agbh]¢ . Thus the set of budget constraints for the four final states (s1, s2, s3, s4) are:
Note that these constraints imply that:
Now, at the intermediate node sa, we have the budget constraint pa(xah - eah) + qaaah £ qaa0h which translates to:
or, plugging in our terms for afah and agah:
or, recalling from before that qfa = m 1 and qga = m 1 + m 2, then this can be rewritten:
Doing the same for the constraint at node sb (where, recall, qfb = m 3 and qga = m 3 + m 4), we obtain:
All that remains is now to collapse both these intermediate constraints into the initial one. Now, recall that the initial constraint states that p0[x0h - e0h] + q0a0h £ 0, or:
or qf0 = la m1+ lb m3 and qg0 = l a(m 1 + m 2) + l b(m 3 + m 4), then:
or, rearranging a bit:
but notice that the terms in brackets are merely the right-hand sides of our intermediate constraints. Thus, assuming an interior solution at the intermediate nodes, we can impose an equality and have:
so plugging these into our initial constraint:
or, rearranging a bit:
which is the single Arrow-Debreu budget constraint. Thus, the maximizing agent is facing a full set of state-contingent markets with state-contingent prices given by:
Notice that we obtain state-contingent prices not only for the final states (s1, s2, s3, s4), but also for the intermediate states (sa, sb) and the initial state (s0). The meaning of these state-contingent prices follows intuitively as the three-period analogue of our earlier result of the equivalence between Radner equilibrium and Arrow-Debreu equilibrium in the two-period case. The most important thing to note is that our set of state returns, V, is a 4 ´ 2 matrix, i.e. rank(V) < 4 = S. We can nonetheless implement the Arrow-Debreu equilibrium and deduce the appropriate state prices without "complete" asset markets in the conventional sense, but rather by repeated trading of merely two long-lived securities. We should note that it can be shown that the minimum number of long-term assets necessary to implement Arrow-Debreu equilibrium can be deduced from the tree-structure. Recall that in obtaining our solution, we went incrementally backwards, ensuring asset market equilibrium at each intermediate node. Now, in Figure 6, at intermediate node sa, we were facing two future states, s1 and s2, thus in that "subproblem", we needed only to be able to make transfers between states s1 and s2. Thus, to span this (sub)space of state returns, we need at least two assets. Similarly, at node sb, we faced only two future states and thus we also needed merely two assets. Now, if the tree structure was different so that, say, we faced three future states at the node sa, then we would need at least three long-lived assets. This would be true even if we continued to only face two states at the other node, sb. Of course, if we have more time periods, and thus more steps along the way, the tree structure could get rather complicated. In this case, the penultimate nodes may only have, say, two branches into the final states, but a single earlier intermediate node might have three of four branches into other intermediate nodes - thus, at that node, we would need more than two assets. Consequently, we can state the general principle of found by Kreps (1982) in this context: the minimum number of long-lived assets necessary to implement Arrow-Debreu equilibrium is the largest number of branches leaving any node. So, if we had T time periods and the largest number of outgoing branches faced by any of the intermediate nodes was two, we would still only need two long-lived assets to implement Arrow-Debreu equilibrium. Duffie and Huang (1985) generalize this principle to continuous time with infinitely many states. Finally, we should mention that asset prices here exhibit what is called the martingale property for asset prices identified by Harrison and Kreps (1979). The martingale property means that the price of an asset at any node is the conditional expectation of the returns in the final states. We can this applies to our case. Let p = (p 1, p 2, p 3, p 4) be the probabilities of the final states s1, s2, s3, s4 from the initial time period; for our case, (as we saw earlier), we can take these to be the Arrow-Debreu state prices, p = (la m 1, la m2, lb m3, lbm4). As a result, the martingale property implies that at the initial state s0, we have (for asset f):
which, if rf = [1, 0, 1, 0] reduces to our earlier qf0 = la m1+ lb m3. The analogous is true for the asset g, where rg = [1, 1, 1, 1], which implies that qg0 = l a(m 1 + m 2) + l b(m 3 + m 4). Now, the conditional probabilities of the final states given that we have achieved node sa, will be pa = (m 1, m 2, 0, 0) while the conditional probabilities of the final states given that we have achieved node sb will be pb = (0, 0, m 3, m 4). Thus the martingale property implies that:
which, again, if rf = [1, 0, 1, 0], implies our earlier qfa = m 1 and qfb = m 3. The analogous case applies for the returns of asset g, where rg = [1, 1, 1, 1], so qga = m 1 + m 2 and qgb = m 3 + m 4. Thus, clearly, we have the martingale property in our asset prices. The martingale property takes on its full force in the context of continuous time and continuous states. For more details, consult the standard references given earlier.
|
All rights reserved, Gonçalo L. Fonseca