Economists talk a lot about "equilibrium". Roughly, this is defined as the situation in an economy when there are "no incentives to change". Yet casual observation of reality tells us that change is always happening: prices are constantly moving up and down, new businesses are set up while others go bankrupt, people are being fired here and hired there, etc. This does not look like the "equilibrium" economists keep talking about, so why bother with it?

Yet, we are told, equilibrium is interesting because it supposedly forms a "gravitational center" for an economy. Economies are said to move towards an equilibrium over time. All the complicated changes that are happening in the "real world" are, allegedly, merely adjustments of some sort or another towards that equilibrium. If nothing else intervenes, these adjustments will eventually take the economy there.

The belief that the economy has a gravitational center was inspired, in good part, by analogy with Newtonian mechanics. Consequently, it ought to be of no surprise that the concept of "equilibrium" -- and its stability -- entered economics during the Enlightenment era. The works of Richard Cantillon (1755), Sir James Steuart (1767) and, of course, Adam Smith (1776) are perhaps the most explicit examples. Smith, for instance, speaks about the relation between "market" (observed) price and the "natural" (equilibrium) price in precisely these terms:

The fact that nothing, as yet, has quite displaced the idea of a gravitational center does not mean that economists hold an unbridled faith in it. Many have suggested alternative organizing concepts. The most famous is the concept of an "evolutionary" system, where the economy is always changing without exactly "ending up" anywhere or even "tending" to any specific point. Thorstein Veblen (1898) strongly advocated that economics should abandon the mechanical analogy in favor of the evolutionary analogy.

Yet the notion of a gravitational equilibrium is hard to displace, not because it seems "correct" or that there is overwhelming empirical evidence for it, but rather because, as economists like to say, it makes analysis "tractable". This invokes, of course, the old story of the man looking for his lost keys under the lamp-post. But, in a sense, it is almost inevitable. As long as alternative concepts, such as evolution, remain contentious, obscure and difficult to handle, the notion of a gravitational equilibrium will probably remain the central organizing concept of much of economics.

At any rate, the concept of equilibrium is already complicated enough as it is. For if a system can be in "equilibrium", then something must be said about how it looks like in "disequilibrium". Yet here there are deep disagreements among economists, even among those within the same school of thought. What exactly does "disequilibrium" mean? At a naïve level, the answer seems clear: if an equilibrium is defined where there are "no incentives to change", then a disequilibrium will be defined as a situation where there are "incentives to change". But it is the responsibility of the economist to be a bit more precise: who has the incentive? what is to be changed? how are the changes actually undertaken? and what are the exact consequences of such changes? Not only do economists generally avoid being specific in providing answers, some do not even dare to ask the questions.

So, how does an economy that is in disequilibrium actually get to an equilibrium position? How does an equilibrium perform its "gravitational" role? This is the question "stability theory" attempts to answer. It is a complicated question and the answers which have been proffered are far from satisfying. Again, this is because disequilibrium tends to be a dreadfully complex thing to describe -- and the economists that have attempted it have tended to confirm that it is so.

In its early years, there were roughly three reactions to the stability question. The first was simply to ignore it because it is expedient to do so. Equilibrium is easier to describe and captures most of what we want to know anyway. This kind of response is exemplified by William Stanley Jevons:

Often appended to such claims is that stability is "self-evident" and does not need to be proved. This happy ignorance has guided much of economics for the past century.

The second answer, implied mainly by Francis Ysidro Edgeworth (1889, 1891), is to ignore dynamics because any explanation that you offer will be inevitably wrong. In this view, it is pointless to attempt to be specific about disequilibrium because disequilibrium is actually not something that is describable. Disequilibrium is not merely one thing, but a description of anything that is "not equilibrium" -- and many, many things are "not equilibrium". One simply cannot hope to characterize disequilibrium by listing all the "incentives to change" because who has the incentive and how the changes are undertaken can vary from situation to situation. As a result there is no "one way" of getting from disequilibrium to equilibrium; it can happen by many different routes and through many different mechanisms. In the Edgeworthian view, then, it is pointless to try to reduce adjustment to a single control mechanism.

Even if we take the ambitious route of assuming many control mechanisms, we run into trouble. With so many machines running at the same time, the system becomes very sensitive to slight changes in specification and it is impossibly hard to predict the path the economy will take as a result. As such, Edgeworth reaches his astounding conclusion that:

The third reaction, exemplified by Léon Walras (1874), is to cut through the Edgeworthian knot by imposing a single control mechanism on the economy. This mechanism is that nebulous entity known popularly as "the market" -- or what economists, in an anthropomorphic fit, have characterized as the "Walrasian auctioneer". The Walrasian auctioneer searches for equilibrium prices guided by nothing but a single mechanism. This mechanism is the Law of Excess Demand: that prices must be raised in markets where there is excess demand and lowered where there is excess supply. The Walrasian adjustment process is also known as tâtonnement ("groping").

This is a deep modification of the concept of "incentives". In the Edgeworthian world, individuals trade with each other, and thus it is they who face incentives and responsibility for changing things if they have the incentive to do so. In the Walrasian world, individuals do not trade with each other, but rather with an abstract entity, "the market". Walras delegates all incentives to "the market" and all the responsibility for changing things to "the market".

Walras's artificial device of a "market" or "auctioneer" mechanism may seems to stretch credulity. If we care to look, we will find no such animal in the real world. Furthermore, the attendant assumptions necessary to make the mechanism work -- e.g. price-taking behavior, etc. -- are no less difficult to swallow. But Walras was not theorizing in a vacuum. As noted earlier, his view of stability possesses a quite distinguished and ancient pedigree, from Cantillon on down. Any honest observer would have to admit that Walras's only sin was to make this control mechanism precise and explicit -- and thereby reveal the tenuous assumptions underlying it.

For the details of the tâtonnement mechanism, Walras drew inspiration from the price-setting operations of the Paris Bourse (Stock Exchange) in the 19th Century (Kregel, 1995). State-certified but independent brokers would periodically arrive at the Bourse with a carnet, listing the orders of their clients. A central "crier" would call out prices, to which the brokers would express the size of their bids and offers. If these did not match, the crier would call out another price and the process would continue until a single price was settled upon that cleared all the trades in the brokers' carnet. The rules in Paris have changed since then. However, this tâtonnement process of price-determination is still followed in the modern London Gold Market (Smith, 1987).

For Walras, the working rules of the Paris Bourse were ideal for price-determination. As he explains:

But it is one thing to say that this is the best organized market, and another thing to say that it can be extended, by analogy, to the rest of the economy. For this Walras did not quite have a ready argument. He did not necessarily believe that such an auctioneer actually existed in the economy in general. Rather, Walras argued that the true mechanism of a competitive market system, while substantially different in detail, nonetheless operated in a similar manner or obtained the same result as the "auctioneer" scenario. Of course, this is not watertight logic. Walras fudged this a bit and never really proved it was the case -- leaving it for his disciples to search not only for a proof, but also for a justification.

After Walras, not much was done with stability. The rest of the Lausanne School -- Barone, Antonelli, Pareto, etc. -- did little more than merely restate Walras's theory. As is well known, Francis Ysidro Edgeworth (1881) proposed a very distinct stability mechanism which deserves its own, separate treatment. Alfred Marshall (1890) was perhaps the only other economist in the late 19th Century to take stability seriously. He worked ostensibly with a different notion, one that relies on different layers of time and motion. It was not as clean and precise as Walras's, but it was just as ambitious.

Yet, for the next fifty years or so, stability practically disappeared from the economist's atlas of theories. Dynamics, of course, did not disappear. Theories of growth and the business cycle continued apace, particularly in the 1920s, so at least some sort of analysis of changes in an economy over time was going on. But these "dynamics" were not really "adjustment" mechanisms; they were not necessarily going anywhere in particular. They were just dynamic processes.

The connection between dynamic process theory and equilibrium theory was never made very clear by these early researchers. On the one hand, we have Henry L. Moore (1925, 1926) identifying the "trend" of the cycle with the (moving) "equilibrium" implied by the Walrasian equations. (cf. Fig. 1, where p(t) is the price cycle, and p*(t) is the trend/equilibrium price path). However, he tells us very little about the mechanisms that actually make equilibrium the trend in a dynamic process and keep the true dynamic path orbiting around it.

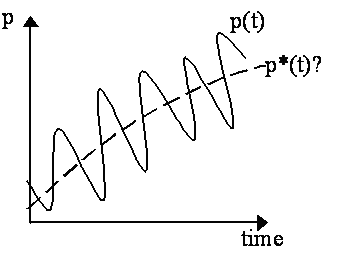
Fig. 1 - Equilibrium as Trend ("Stability of the Second Kind")

An alternative view was that the Walrasian equilibrium might somehow be related to the "stationary state", i.e. the point in the dynamical process when there are no more changes (cf. Fig. 2). In a revealing article, Lionel Robbins (1930) argued that the equilibrium of economists should be formulated as the outcome, the "stationary state", of some dynamical process. This point was reiterated forcefully by Ragnar Frisch (1933, 1936) and Arthur Smithies (1942).

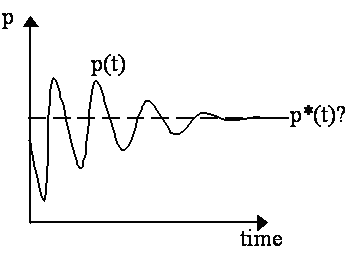
Fig. 2 - Equilibrium as Stationary State ("Stability of the First Kind")

In one sense, this is obvious. What is an "equilibrium" if not the balance of dynamic forces tending against each other? But, in another sense, it rules out "unstable" equilibria. This reasoning would lead one to conclude, using Edgeworth's famous analogy, that a ball at the bottom of a bowl is "in equilibrium". But a ball perched on top of a hill is not in equilibrium because there are no dynamic forces that could take the ball there (Fig. 3). This second case is an "unstable" equilibrium. But is an "unstable" equilibrium an equilibrium all the same? A perfectly-perched ball will not move, there are no incentives to change, and so by definition it is an equilibrium. However, if we define equilibrium as a stationary state This is consistent with Knut Wicksell's claim that "[i]f [instability] is the case, no real equilibrium of the price exists, but only a temporary equality of supply and demand." (Wicksell, 1893: p.87).

Fig. 3 - Bowl and Hill: Stable and Unstable Equilibria

In the 1930s, the idea that a Walrasian equilibrium should be modeled as the stationary state of some dynamic process brought forth a whole new set of interesting problems. An equilibrium is defined by some set of data (preferences, endowments, technology, etc.), then if an equilibrium is to stay put while the dynamic path approaches it, that means that the underlying data must remain constant all the while. If the data changes before the equilibrium is reached (a real possibility if the stability process takes time), then the equilibrium will move and the path must be redirected. It is questionable, under these conditions, whether such a dynamic process will ever reach an stationary point at all! And, even if it does, the equilibrium reached might depend on the precise path followed. Nicholas Kaldor (1934) was perhaps the first to alert economists to the likelihood of this result.

Léon Walras (1874) might have realized this possibility himself. However, he still believed that, despite the moving equilibrium, the dynamics were governed by an "adjustment-to-equilibrium" mechanism. As Walras writes:

It seems, then, that Walras believed that even though the equilibrium is shifting around because of changes in data, the dynamics are still governed by the tâtonnement process -- a fruitless mechanism, of course, because, in a continuous market, the auctioneer never actually reaches the particular equilibrium he is groping for. But in Walras's eyes, tâtonnement was still the only dynamic mechanism, even if the equilibrium did not stay put. Using our analogy, if we keep shaking the bowl, the ball may never reach the bottom, and even if it does, it is not bound to stay there. But the dynamic force governing the ball's movement towards the bottom of the bowl remains true, whether the bowl stands still or is shaken around. The laws of gravitational mechanics may be rendered predictively useless in a shaking bowl, but they are not contradicted or invalidated. They are just incomplete.

So, there are actually two dynamic processes going on simultaneously in a "continuous market" -- one (unmentioned) changing the data and thus the equilibrium, and another (tâtonnement) adjusting to equilibrium. We know how to model the second mechanism, but how do we model the first? Stretching our analogy, to understand the true dynamics of a ball in a shaking bowl, it is not enough to appeal to a dynamical theory of a ball-in-the-bowl; it is also necessary to provide some theory of the shaking.

Walras does not identify precisely the source of the changes in data. Ragnar Frisch (1933, 1936) and Arthur Smithies (1942) did this quite simply. They coupled a precise and well-determined adjustment-to-equilibrium mechanism with a series of "random" changes in the underlying data. Their "theory of shaking" was thus of the simplest nature possible: randomness.

However, some economists expressed serious doubts about this type of resolution because it leaves the dynamics open-ended. For Frank Knight (1930), in particular, changes in the data conformed to some historical patterns of "social evolution" and even if these are "beyond the province of the economic theorist", they are hardly random. From a different angle, by Adolph Löwe (1926) and Simon Kuznets (1933) argued that both the source of the changes in data as well as the adjustment mechanism should be accounted for in a single, "self-contained" system.

A special case of this phenomenon is path-dependence of equilibrium, first identified by Nicholas Kaldor (1934) and resurrected by Don Patinkin (1956). If the stabilization process takes time, it is logical to suppose that some exchange will happen in the interim. But, as we know, any exchange that happens out of equilibrium will change the "data" of the problem (i.e. endowments are swapped, some wants are satisfied, etc.), so that a whole new equilibrium is called for. As Patinkin explains,

"the intermediary purchases which are carried out must affect the nature of the market excess-demand functions which determine the subsequent evolvement of the tâtonnement. In particular, the set of prices which prevails when the market is finally cleared depends on the time path of the tâtonnement as a whole and will, therefore, not generally be the same for any two tâtonnements." (Patinkin, 1956: p.532-3).

Notice that this path-dependence is not quite what Frisch or Smithies or even Knight had in mind. Because out-of-equilibrium exchange is governed by the "false" prices in the economy at that moment, then the changes in data are actually endogenous. We consequently enter into a cat-and-mouse situation, where the path is chasing a fugitive, moving equilibrium -- whose very movements are in a sense caused by the approaching path itself.

[Note: There are good reasons to suppose that Walras himself recognized this, which is why he introduced the device of "tickets" in his book. For more on what Walras really meant by this, see the ensuing debate in Goodwin (1951), Patinkin (1956), Morishima (1977), Jaffé (1967, 1981), Walker (1987, 1996) and Kompas (1992).]

All these results lend confirm our initial doubt that the dynamic process should be modeled as a process of "adjustment" to begin with. Perhaps a return to Veblen's "evolutionary" conception of dynamics might be necessary after all.

John Hicks, in his seminal treatise Value and Capital (1939), took the tentative first steps of integrating dynamic theory with Walrasian general equilibrium theory. Hicks's motives and concerns were driven partly by his reading of the equilibrium theories of Walras and Pareto and partly by his familiarity with the sequential "process" theories of Lundberg and Robertson. He ended up with two sorts of dynamic theory: a "short-run", tâtonnement stability theory that solves the equilibrium of a "day" (when data is constant), and a longer-run, week-to-week, sequential process related to expectations adjustments and data changes.

It was the tâtonnement part of Hicks's theory that made a big splash among contemporaries. In the appendix to Value and Capital, Hicks examined the conditions for "local tâtonnement stability" of a Walrasian general equilibrium system in a rather peculiar way, holding some markets constant while adjusting others. Paul Samuelson (1941, 1942, 1944), then a young blade, criticized Hicks's method for not being "true dynamics", i.e. that his theory of adjustment had not been explicitly related to a mathematically-coherent dynamical process.

Paul Samuelson (1941, 1942, 1944, 1947), Oskar Lange (1942, 1944) and Lloyd Metzler (1945) reformulated the stability question in its "true" dynamic form as a system of differential equations. The question was also taken up independently by Maurice Allais (1943) and Takuma Yasui (1948).

Metzler demonstrated that one of the critical conditions guaranteeing local stability of equilibrium is that all commodities must be gross substitutes. This, of course, is far too strict an assumption. The Hicks-Metzler conditions were further loosened by Frank Hahn (1958), Takashi Negishi (1958), Kenneth Arrow and Lionel Hurwicz (1958) and Lionel McKenzie (1960). Considerations also emerged of the global stability of equilibrium and the associated question of uniqueness. The seminal contribution here was Arrow, Block and Hurwicz(1959).

However, through a set of illustrative examples, Herbert Scarf (1960) and David Gale (1963) demonstrated that the tâtonnement stability conditions were not reasonable conditions. They were far more restrictive than most economists would be willing to accept. In other words, there are many perfectly reasonable economies which do not meet the conditions required for stability. The despiriting Scarf-Gale examples were further reinforced by the results of the Sonnenschein-Mantel-Debreu Theorem that emerged in the early 1970s.

Another line of attack was pursued by Stephen Smale (1976), utilizing the global Newton method. Smale basically sought to determine a price-adjustment mechanism that converges to equilibrium for almost all economies. However, Smale's auctioneer requires a lot more information about excess demands than the original Walrasian auctioneer. Saari and Simon (1978) tried to determine the minimal amount of information a Smale-type auctioneer would need to be sufficiently effective. Unfortunately, they found that the informational requirements remained substantial.

Frank Hahn (1962), Hahn and Negishi (1962) and Hirofumi Uzawa (1962) opened up a different avenue, namely the study of non-tâtonnement stability mechanisms, i.e. mechanisms that allowed for out-of-equilibrium exchange. This remained a cottage industry in its own right through to the 1970s . With non-tâtonnement mechanisms, equilibrium is path-dependent. In other words, the adjustment mechanism does not, generally-speaking, converge to the Walrasian equilibrium of the initial economy. As such, strictly-speaking, they is not really analyzing the "stability" properties of a Walrasian equilibrium, but rather merely proposing processes of convergence to a Pareto-optimal allocation. While perhaps more realistic, their connection with Walras's theory of equilibrium remains tenuous at best.

A related tradition is the dynamics of Leontief-von Neumann general equilibrium systems. In this case, the traditional Neoclassical cross-dual laws of adjustment are replaced with a set of direct dual laws of adjustment. In the direct dual laws, prices move in response to excess profitability (Classical competition) while quantities move in response to excess demands (Keynesian multiplier). The pioneers in this tradition include Michio Morishima (1959, 1964), Robert Solow (1959) and Dale Jorgensen (1960, 1961).

If anything was revealed in this research program, it was that, as alluded earlier, economists had not come to an agreement on how equilibrium was supposed to be reached. The sensitivity of the resulting equilibrium to the particular mechanism assumed and path that was followed, made agreement all the more difficult. A pessimistic assessment of the state of the art was given in Frank Hahn's 1970 presidential address to the Econometric Society:

"It must now, I fear, be admitted that the study of the Walrasian "groping" or tâtonnement proces has not been very fruitful. It was hoped that, by considering a situation so drastically simplified by the supposition of "recontract" or no exchange, it would be possible to lay bare the essentials of the law of "supply and demand" and that once revealed, they would be found to be "good". What has been achieved is a collection of sufficient conditions, one might almost say anecdotes, and a demonstration by Scarf and later by Gale, that not much more could be hoped for." (Frank Hahn, 1970: p.2)

In the 1980s and 1990s, stability questions were gradually thrown onto the backburner. The general decline in interest in general equilibrium theory during this period may account partly for this neglect. But the main reason was probably the growing popularity of the notion of an "intertemporal equilibrium", which gives a distinctly different role for time. An "equilibrium" was no longer conceived as something that is to be reached over time, but rather became something that is itself defined over time. Perfect foresight and rational expectations eliminated even the little scope for stability analysis that this intertemporal notion offered by positing that agents would force the economy to automatically and instantaneously "jump" to the equilibrium path with no more ado.

By and large, these intertemporal developments precluded more serious considerations of the stability question. But they have, by no means, killed it off. After the 1980s came to an end, Frank Hahn struck an optimistic note about the chances of a renewed concern with stability theory:

"When Samuelson criticised perfect stability and proposed a "true" dynamics he started a hare which many of us proceeded to chase. As it turns out that chase (in the case of tâtonnements) ended up in a cul de sac. Had we paid more attention to the analysis of Part III of [John Hicks's] Value and Capital we might have been more circumspect. There it is clear that the important elements of dynamics are to be found in production decisions and in expectations formation....Time has been wasted by rational-expectation-equilibrium theorists because of a lack of understanding of these matters. However that episode too seems behind us. We are now, one hopes, set to work again on Part III of Value and Capital." (F.H. Hahn, 1991: p.82)

Indeed, in recent years, there has been something of a resurrection of the tâtonnement mechanism in light of the rise of non-linear complex dynamics. Day and Piaganini (1991), Bala and Majumdar (1992), Weddepohl (1995) and Goeree, Hommes and Weddepohl (1997) and Tuinstra (2001) are examples of this renewed interest.