|
_________________________________________________________________
_________________________________________________________________
Contents (1) Problems in the Walras-Cassel Model [For alternative presentations, consult Kuhn (1956), Dorfman, Samuelson and Solow (1958: Ch. 13), Karlin (1959), Lancaster (1968: Ch.9) and Weintraub (1983)]. (1) Problems in the Walras-Cassel Model Recall that in the simplest Walras-Cassel system we had the following set of equations:
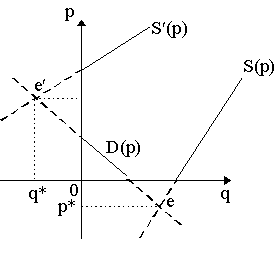
If we have n produced goods and m factors, then have n equations in (i), m equations in (ii) and n equations in (iii), but as we can always remove one equation by Walras's Law, then we have a total of 2n+m-1 equations. The unknowns in this system are x (n unknowns), p (n unknowns) and w (m unknowns), and, by the numeraire, we could omit one of these, thus we would have total of 2n+m-1 unknowns. The first problem we obtain with Walras's method of solution is that setting the number of equations equal to the number of unknowns is neither necessary nor sufficient for the existence of a solution. It is not sufficient because xy = 3 and x + y = 1 are two equations with two unknowns which has no real solution. Furthermore, it is not necessary because, for instance, x2 + y2 = 0 has a unique solution, but it is one equation with two unkowns. Heinrich von Stackelberg (1933) pointed out this difficulty and noted the following: namely, if the number of industries using a particular set of factors is less than the number of factors, it is conceivable that prices and quantities become indeterminate. His objection can be illustrated directly by supposing that we have merely one industry and two factors, so that p = b1w1 + b2w2 is the only price-cost equation. Clearly, this has no solution: there are numerous combinations of w1 and w2 that can yield the same output price p (in terms of our earlier diagram, we would only have one P-locus in our two-dimensional factor price space). This problem would not arise if we had two outputs: as we illustrated with our simple two-sector Walras-Cassel system and outputs in this case are quite determinate. Thus, Stackelberg indicated, for determinacy, we need at least the condition that n ³ m. More specifically, we need to ensure that if there are m factors, then there must be at least m industries which use all m factors. The reason for the strength of this last statement can be gathered if we have, for instance, four outputs (x1 to x4) and four inputs (v1 to v4), where industry x1 uses factors v1 and v2 exclusively while industries x2, x3 and x4 use combinations of the remaining factors v3 and v4. Thus, even though n = m as a whole, notice that because factors v1 and v2 are only used by one industry (x1), the indeterminacy problem remains. Another problem emerges in this example which was also noticed by Stackelberg: namely, if we have three industries (x2, x3 and x4) which use two factors (v3 and v4), we cannot guarantee that the Walras-Cassel conditions will be met. Heuristically, imagine three price locii in a two-dimensional factor returns space: it is highly improbable that all three price locii will intersect at a single point. In other words, there is (probably) no combination of the two factor returns where all the price-cost equations are satisfied. Noticing this, Stackelberg suggested that we must allow for some of the equalities to remain unsatisfied. As was first pointed out by Hans Neisser (1932), the imposition of the equalities (ii) v = B¢ x and (iii) p = Bw yields another troublesome issue. If factor supply must equal factor demand, it is entirely conceivable that this holds at negative prices for some factors. (heuristically, see Figure 1, where for a particular market, demand D(p) and supply S(p) intersect at e, yielding negative equilibrium price, p*). Similarly, if prices must equal cost of production for every commodity, then we are not excluding situations where this condition is met at negative levels of output for some commodities (cf. Figure 1, where D(p) and S¢ (p) intersect at e¢ , yielding negative equilibrium output, q*). Yet while negative prices and negative quantities are entirely possible they are not economically meaningful.
Friederik Zeuthen (1933) was the first to explicitly suggest that inequalities be introduced into the Walras-Cassel system so that "free goods" could be admitted. As Zeuthen notes, the Walras-Cassel system imposes the arbitrary assumption that all factors are scarce and thus that all have "prices". However, a factor is scarce only if there is more demand for it than is available - hence the price. But it is conceivable, Zeuthen noted, that a factor may be so plentiful or demand for it so minimal that it is not scarce (i.e. supply exceeds demand at any positive price, e.g. S(p) and D(p) in Figure 1) and thus that factor should have a zero price. In any case, one cannot decide a priori which factors are to be free and which are not. As Zeuthen reminded everyone the decision as to which commodities were "economic" and "non-economic", as Carl Menger (1871) had taught long ago, should be result of the equilibrium and thus endogneous to the problem. As he writes, "one does not know at the outset which goods are free goods, so one should insert into the equality the possibility of an unused residual and, at the same time, stipulate among the conditions that either this residual or the price of the resource equals zero." (Zeuthen, 1933). (2) Schlesinger-Wald Inequalities and Shadow Values The participants of the Vienna Colloquium, notably Karl Schlesinger (1935) and Abraham Wald (1935, 1936), followed up on the Neisser-Stackelberg-Zeuthen critique of the Walras-Cassel system by introducing inequalities into the factor market clearing equations. Thus, allowing for an inequality in the factor market equilibrium condition, we obtain:
so that, in equilibrium, for a particular factor j, either the quantity supplied of that factor is equal to the quantity demanded (i.e. vj = Bj¢ x) or the quantity of that factor supplied exceeds the demand for the factor, vj > Bj¢ x, but then the corresponding return to factor j must be zero, i.e. wj = 0. Although in the context of a different model, John von Neumann (1937) adopted the quantity inequalities suggested by Schlesinger and Wald, but also introduced one that they had not thought of: namely, that price-cost equations should also be transformed into inequalities in order to allow for "non-produced" goods. Translated into the Walras-Cassel context, this implies that we ought to have in equilibrium:
so that, in equilibrium, for a particular good i either its price is equal to its cost of production (i.e. pi = Biw) or its price is less than cost of production, pi < Biw, but then the corresponding amount of good i produced is zero, i.e. xi = 0. As we see, the Schlesinger-Wald-von Neumann inequalities allow that, in equilibrium, some factors may not have value and some goods may not be produced at all. In this way we will be guaranteed that there will never be negative prices nor negative quantities in equilibrium. In place of these, we will have "free factors" and "non-produced goods". Now, Walras himself had been aware of this problem, but feared replacing equalities with inequalities because then his number of equations would fall below the number of unknowns in the system. As the mathematics of linear and non-linear programming were undeveloped during his time, Walras effectively felt that he had to impose equalities in order to obtain a determinate solution. It was up to Abraham Wald (1935, 1936) to show that this was not necessary and that existence was possible when these inequalities are introduced. The basic insight is that we can decompose our equilibrium conditions into a linear programming problem with a primal and a dual. The primal is:
where we are maximizing output revenue, p¢ x, subject to the constraint that factor demand (B¢ x) not exceed factor supply (v). Thus, from the primal problem, given p, v and B¢ , we obtain the solution x*. As any standard linear programming text shows (e.g. Takayama, 1974), the primal can be rewritten as a Lagrangian problem L = p¢ x + l[v - B¢ x] where l is an m ´ 1 vector of Lagrangian multipliers. The "solution" to this is then a pair (x*, l*) where
Let us now turn to the dual problem. This is:
where we are minimizing returns paid to factors w¢ v, subject to the constraint that cost of production (Bw) not fall below output price, p. Thus, in the dual problem, given p, v and B, we obtain the solution w*. We can also express the dual problem as a Lagrangian L = w¢ v + m[Bw - p] where m is a n´ 1 vector of Lagrangian multipliers. The solution to this problem is a pair (w*, m*) where:
The duality theorem of linear programming (e.g. Gale, 1960: p.78; Lancaster, 1968: p.29; Takayama, 1974: p.156) claims then the following three results:
This last condition (iii) is extraordinarily important - as these complementary slackness conditions replace the market-clearing and price-cost equality conditions for equilibrium and allow situations of free goods and non-produced outputs outlined earlier. The first complementary slackness condition, w*[v - B¢ x*] = 0, means that for every factor j = 1...m, either markets clear (so vj = Bj¢ x* = 0) or some factors are in excess supply (vj > Bj¢ x*) - but if the latter is true, then the complementary slackness condition requires than that wj = 0 (the factor in excess supply is free). Thus, wj > 0 only if vj = Bj¢ x*, i.e. a factor earns positive returns only if the market for that factor clears. If vj > Bj¢ x*, then that factor must be free. Conversely, the second complementary slackness condition, x*[Bw - p] = 0, means that for every produced good i = 1, ..., n, either price equals cost of production (so pi = Biw*) or price is less than cost of production (pi < Biw*), but if the later is true, then the complementary slackness condition requires that xi = 0 (the corresponding level of output of that good is zero). Thus, xi > 0 only if pi = Biw*, i.e. a good is produced at a positive amount only if its price equals its cost of production. If pi < Biw* for a particular good i, then that good is not produced. The shadow values are even more interesting than they seem. In principle, the shadow values of any programming problem - i.e. the Lagrangian multipliers -- refer to the gain the optimized value of the objective from a marginal release in the relevant constraint. For the primal problem max p¢ x s.t. v ³ B¢ x, the Lagrangian multiplier l j* denotes the gain in p¢ x* when the jth factor supply constraint is slightly released, thus:
This expression can be interpreted as the marginal value product of factor j: i.e. the increase in the maximal revenue (prices times maximal outputs) from a marginal increase in the supply of factor j. Using the duality theorem, we know that l j* = wj*, thus the Wald program yields the solution that ¶ p¢ x*/¶ vj = wj, i.e. the jth factor's return (wj) is equal to its marginal value product! Thus, in effect, the duality theorems have resurrected the marginal productivity theory of distribution! The complementary slackness conditions reinforce this intuition: as wj*[vj - Bj¢ x*] = 0, then the jth factor will not be paid anything if it is in excess supply in equilibrium. In other words, if a factor is not scarce, its marginal value product will be zero (i.e. if the factor constraint is not binding, then adding more of the factor will not increase marginal value product) and, consequently, it will not be paid anything. This result has been historically somewhat surprising. For a long time, many economists supposed that marginal products were not defined unless the production function was differentiable with continuous substitution among techniques, etc., and that consequently fixed proportions technology would not yield the marginal productivity theory of distribution. Even Friedrich von Wieser (1889), who had initially announced that factor prices were determinate with fixed coefficient production technology, doubted that the marginal productivity theory would be met. An interesting historical aside relates to the Soviet economist and pioneer of linear programming, Leonid Kantorovich. Kantorovich obtained many of these results in the 1950s, yet feared that they might compromise his status in Soviet Russia. Consequently, when he published his results (e.g. Kantorovich, 1959), he buried them in a mountain of heavy Marxian jargon -- e.g. referring to the Lagrangian multipliers as "objectively determined evaluations" -- lest he be accused of lending credence to the Neoclassical marginal productivity theory. The analogous exercise for the dual problem, min w¢ x s.t. p £ Bw, is no less interesting. Here, the Lagrangian multiplier m i* refers to the reduction in the optimal w¢ *v when the ith output price constraint is released, i.e.
which can be interepreted as the increase in minimum costs given a rise in the price of good i. Using the duality theorem, m i* = xi*, thus we obtain the solution that ¶ w¢ *v/¶ pi = xi*. This can be thought of, in effect, as a version of the famous Hotelling's Lemma. (3) A Simple Graphical Illustration The linear production conditions of the Wald system can be illustrated using the same two-sector model we employed earlier in the Walras-Cassel model. We have two outputs, x1 and x2, and two factors, v1 and v2. Output prices are p1, p2 and factor prices are w1, w2. Technology is given by the unit input coefficients b11, b12, b21, b22. The primal problem, can now be written as:
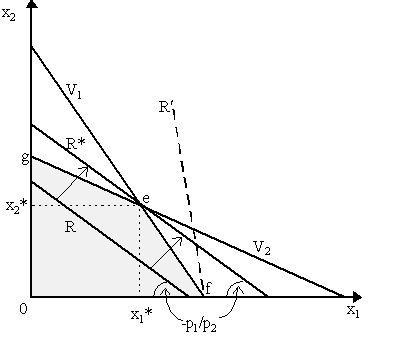
This is illustrated for this case Figure 2 below. The factor market inequality constraints permit us form a feasible region, shown in Figure 2 as the shaded area below the curves V1 and V2 (where, recall, V1 is where the locus of output levels, x1, x2, where the first constraint is met with equality and V2, where the second constraint is met with equality). The condition x1, x2 ³ 0 ensures that the feasible region is above the axes. The objective in the primal problem is the maximization of total revenue, p¢ x, where p is given exogenously. Thus, letting R be a given amount of total revenue, we can define a linear locus R = p1x1 + p2x2 depicted in Figure 2 by the straight line denoted R. This line represents the combinations of x1 and x2 which, for a given set of prices p1 and p2, yields total revenue R. The locus R can be rewritten as:
thus it has negative slope -(p1/p2) and vertical intercept R/p2 (and horizontal intercept R/p1). In Figure 2, the higher locus R* denotes the combinations of x1, x2 points which, for the same prices p1/p2, yields the higher revenue R*.
With prices p1, p2 given, then the primal problem will yield the solution x* = (x1*, x2*), shown in Figure 2 by point e. This represents the highest locus R* which meets the constraints imposed by factor market clearing. Notice that in Figure 2 this happens to be at the corner point e in Figure 2 which lies on both the V1 and V2 locii, thus both constraints are binding, v1 = b11x1* + b12x2* and v2 = b21x1* + b22x2*. However, it is not necessary that the solution to the primal problem yields market clearing. For instance, suppose output prices were such that the revenue locii were much steeper (e.g. R¢ in Figure 2). In this case, the solution would be a corner point such as f in Figure 2. Notice that at f, the V1 locus is binding (thus v1 = b11x1* + b12x2*), but we are clearly below the V2 locus (thus v2 > b21x1* + b22x2*). Thus, at these new output prices, the revenue-maximizing problem yields a solution where we have market-clearing for factor v1 and excess supply of factor v2. Notice also that at f, we produce no output of good x2. We can trace a relationship between the output price ratio p1/p2 and the solution x* to the revenue-maximization problem by recalling that the slopes of the V1 and V2 constraints in Figure 2 are -(b11/b12) and -(b21/b22) respectively, where (b11/b12) > (b21/b22), which translates into saying that ouput x1 is relatively v1-intensive in output x2 is relatively v2-intensive. Consequently, when p1/p2 is very high (i.e. the revenue curves are very steep), so that p1/p2 > (b11/b12) > (b21/b22) then the solution will always be the corner solution f in Figure 2, where a positive amount of good x1 and no amount of good x2 is produced and where factor v2 is in excess supply, but v1 is market-clearing. Notice that if it happens that p1/p2 = (b11/b12) so that the revenue curve is of exactly the same slope as factor constraint V1, then any point on V1 between e and f will be considered optimal. Thus, in this case, the output levels are indeterminate (x2 ranging somehwere between 0 and x2* in Figure 2, x1 ranging from x1* to f), but we are certain that, except for point e itself, the factor v2 will always be in excess supply and factor v1 will be at market-clearing. Conversely, if output prices are such that the revenue curve is flatter than the V2 constraint, then the solution will be g in Figure 2, where V2 is binding and V1 not binding. The following table gives a breakdown of the different types of solutions we would obtain in Figure 2 depending on the slope of the revenue curve (i.e. output prices p1/p2). We go from steepest to flattest revenue cure:
Notice that in Table 1, we only obtain indeterminacy in output levels when output prices are exactly such that the slope of the revenue curve is identical to V1 or V2, otherwise output levels are clearly defined. Let us now turn to the dual problem. The dual for this two-factor, two-output case is:
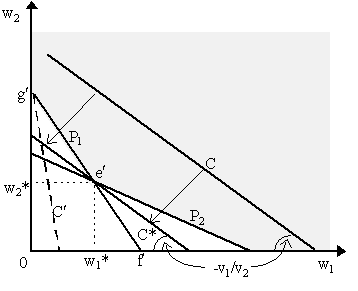
which is illustrated in Figure 3. The price-cost inequalities for the two production processes create a feasible region, represented in Figure 3 by the shaded area above the curves P1 and P2. The lines P1 is the locus of factor prices, w1, w2, where the first constraint is met with equality and P2 is the corresponding locus for the second constraint. The condition w1, w2 ³ 0 ensures that the feasible region does not stretch below the axes. The objective in the dual problem is the minimization of total factor payments, wv, where factor supplies v = (v1, v2) are given exogenously. Thus, letting C be a given amount of total factor payments we can define the locus C = w1v1 + w2v2 depicted in Figure 3 by the straight line C, which represents the combinations of factor prices w1 and w2 which, for a given set of factor supplies (v1, v2), yields the same costs C. The locus C can be rewritten as:
and so has negative slope -(v1/v2) and vertical intercept C/v2. In Figure 3, the lower locus C* represents the combinations of factor prices which, for the same factor supplies, yields lower total cost C*.
The analysis proceeds in an analagous manner. With factor supplies v1, v2 given, the dual problem will yield the solution factor prices w* = (w1*, w2*) in Figure 3 at point e¢ , the lowest cost locus C* which fulfills price-cost constraints. As e¢ it is on the corner of P1 and P2, then both constraints are binding, p1 = b11w1* + b21w2* and p2 = b12w1* + b22w2*. However, once again, this need not be the case. If factor supplies are such that the C locus is quite steep (C¢ in Figure 3), then the solution will be a corner such as f¢ in Figure 3. Notice that at this corner, P1 is binding but P2 is not, so p1 = b11w1 + b21w2 and p2 < b12w1 + b22w2, i.e. price equals cost of production for output x1 (thus production of x1 breaks even, or is "viable") but output process x2 is running at a loss. Notice, correspondingly, that at f¢ , factor prices w1 = 0 and w2 = g¢ > 0. If factor supplies were such that the cost locii are very flat, the corresponding solutions will be at g¢ , where P1 is non-binding and thus x1 is running at a loss, but P2 constrains and thus x2 is viable. Recall that the slope of P1 is -(b11/b21) and of P2 is -(b12/b22). The fact that P1 is steeper than P2 indicates that b11/b21 > b12/b22 which, it can be noticed at once, is consistent with the inequalities we assumed in the primal problem earlier depicted in Figure 2. We can trace the relationship between factor supplies (v1/v2) and the solutions to the cost-minimizing problem as depicted in Figure 3. These is laid out in Table 2 below. We go from the case where the cost locus is the steepest to when it is the flattest:
Once again, note that we only obtain indeterminacy in factor prices when factor supplies are such that the slope of the cost curve happens to be identical either to the slope of P1 or P2. Notice also that we have the intuition that when a particular factor price is low, the output process which is relatively intensive in that factor will be viable, whereas when a factor price is high, the output process relatively intensive in that factor will be running at a loss (compare factor price w1 and the viability of the v1-intensive output process x1 or factor price w2 and the viability of the v2-intensive output x2). (4) Existence and Uniqueness of Equilibrium We are not finished, however. The linear programming problems set out above yield us (modified) market clearing conditions (the complementary slackness equations), pure competition and solutions for output (x*) and factor returns (w*) - given a particular technology (B), a price vector (p) and a factor supply vector (v). To assume technology given is not too difficult (although issues of choice of technique are relevant, they would take us too far afield at this point), but where do the given p and v come from? As in the Walras-Cassel model, we need consumer output demand functions and factor supply functions to close the system. Recall that from utility-maximization we obtained market commodity demand functions D(p, w) and market factor supply functions, F(p, w). For simplicity, we shall ignore factor supply functions F(p, w) and assume factors are supplied inelastically (i.e. v is fixed) for the rest of this section. Now we turn to the existence question posed by Abraham Wald (1935, 1936). Consider the equlibrium price vector p*. If we plug this into our primal and dual problems, we obtain solutions x* and w*. Taking these derived factor prices w* and our original prices, p*, we can plug them into our demand function to obtain the quantity demanded, D(p*, w*). If we are indeed in equilibrium, then it would better be that the output levels x* we found in the primal problem be equal to this demand, i.e. D(p*, w*) = x*. If not, then p* could not have been equilibrium to begin with. The existence question is then this: is there indeed a p* such that the w* and x* we obtain as solutions to the linear programming problems will lead us to an equilibrium? Wald proved that indeed such an equilibrium exists although he did not have price-cost inequalities and did not possess the linear programming duality theorems as a weapon. Consequently, shall not replicate his rather complicated proof, but instead take the avenue set out in Lancaster (1968: Ch. 9) (for an alternative proof, see Dorfman, Samuelson and Solow (1958: Ch. 13)). As v is given, then we insert any set of prices p, we obtain, from the primal, a solution x and solution w from the dual. Henceforth, we shall refer to the solution to the primal problem as x(p) and the solution the dual problem as w(p). We shall reserve the terms p*, x* and w* for equilibrium prices and quantities. Let us first confine prices to a price simplex. We know that if p is given, then w(p) is the associated solution in the dual. Consequently, if kp is given, then it can be easily shown that kw(p) is the solution in the dual. Demand is homogeneous of degree zero in output and factor prices, then D(p, w) = D(kp, kw) and the solution to the primal problem is also homogeous of degree zero in output prices, x(p) = x(kp) (i.e. notice in Figure 2 that doubling output prices will leave the slope of the objective functions and thus the solution x(p) unchanged). As a consequence, we can normalize p so that å i=1n pi =1. Thus, let us defined the price simplex P = {p | p ³ 0, å ipi = 1}. We now turn to the following preliminary lemma:
Proof: As x* and w* are the equilibrium outputs and factor prices, then by definition of equilibrium we must have it that p*D(p*, w*) = w*v by the aggregation of the consumer budget constraints. By output-market clearing, D(p*, w*) = x*, thus this can be rewritten as p*x* = w*v. Now, if we insert equilibrium ouptut prices p* into our linear programming problem, we obtain solutions (x(p*), w(p*)) where, by the duality theorem, w(p*)[v - B¢ x(p*)] = 0 and x(p*)[Bw(p*) - p*] = 0 which translates to: p*x(p*) = w(p*)v. It is noticeable from before that equilibrium outputs x* and factor prices w* fulfill this condition, thus they are solutions to the linear programming problems.§ The purpose of the Lemma was to demonstrate that once we know the equilibrium prices p*, we know by extension that the equilibrium outputs x* and factor prices w* will be solutions to the linear programming problem with p* given. As a further note, it worth remembering the following from the duality theorem p*x(p*) = w(p*)v. If the optimal solution w(p*) is indeed an equilibrium factor price vector w*, then from the budget constraint, we necessarily have it that x(p*) = D(p*, w*), i.e. output market clears, so the solution x(p*) is the equilibrium output. Conversely, if optimal solution x(p*) is equilibrium output x*, then, again from the budget constraint, necessarily the solution w(p*) will be the equilibrium factor price, w*. Now, suppose any p is given. Then, we can define the resulting vectors w(p) and x(p) as the solutions to the linear programming problem. In principle, solutions to the linear programming problem are not necessarily unique, thus let us define W(p) and X(p) as the associated sets of optimal solutions - which, note, will be convex. Thus, for any w Î W(p) and any x Î X(p), we have it by the duality theorem that px = wv or, more succinctly, pX(p) = W(p)v. Now, demand vector is defined as D(p, w). As w = w(p) by solution, then we can reduce this to D(p, w(p)) = D(p) as the market demand vector when prices are p. Naturally, many demand vectors may be chosen at a particular price, thus let us define D(p) as the set of demand vectors D(p). Thus, we can now define the set of excess demand vectors at price p as:
Pre-multiplying every vector in this set by p, we have:
Now, since the budget constraint is fulfilled for any D(p) Î D(p), we thus have it that pD(p) = W(p)·v and since pX(p) = W(p)v by the linear programming problem, then this can be written:
which is simply Walras's Law. Now, recall that X(p) and W(p) are mappings from prices to optimal sets in the linear programming problems. Now, as we know from standard programming theory, these will be upper semicontinuous correspondences. In constrast, as we know that D(p) is a continuous function of p, then D(p) is upper semicontinuous. The sum of upper-semicontinuous correspondences will be upper semicontinuous, thus Z(p) must be upper semi-continuous. We would also like to show it is convex. This is easily done with the assistance of Walras's Law.
Proof: Defining Z(p) = D(p) - X(p), we know that Z(p) is a convex, upper semi-continuous correspondence from the price simplex P. By the Gale-Nikaido Lemma, there is consequently a price-vector p* such that Z(p*) Ç (- W ) is not empty. This last implies that there is a z* Î Z(p*) where z* £ 0. We now wish to prove that conditions (1)-(6) are met at z*. Condition (1) is automatic from the Gale-Nikaido lemma: namely, z* £ 0 implies zi* = Di(p*, w*) - xi* £ 0. Condition (2) follows from Walras's Law pZ(p) = 0. As z* Î Z(p*), then p*z* = 0,which can be rewritten for the ith market as pi*[Di(p*, w*) - xi*] = 0, so if Di(p*, w*) < xi*, then necessarily pi* = 0. Condition (3) follows from the definition of X(p). At equilibrium prices, p*, we defined X(p*) as the set of solutions to the primal problem, so by definition as x* Î X(p*), then v ³ B¢ x*, so for the jth factor, (3) follows. Condition (4) follows from the Lemma: as p* and x* are equilibrium prices and outputs, then as we know from the duality theorem, the solution to the dual problem w* will be equilibrium factor prices. Consequently, optimality conditions establish that w*[v - B¢ x*] = 0, thus for the jth factor, wj*[vj - B¢ jx*] = 0, so if vj > B¢ jx*, then necessarily wj* = 0. Condition (5) follows by the same logic. At equlibrium prices p*, we defined W(p*) as the solution to the dual problem, so by definition w* Î W(p*), so p* £ Bw*, so for the ith output, (5) follows. Finally, condition (6) is obtained also from the Lemma: as p* and w* are equilibrium output prices and factor prices, then by the duality theorem, the solution to the primal problem x* will be equilibrium outputs. Consequently, optimality conditions establish that x*[Bw - p] = 0, so for the ith output, xi*[Biw* - pi*] = 0, so if pi* < Biw*, then necessarily xi* = 0. Finally, let us turn to (1¢ ). If we assume B > 0 strictly (all elements positive), then Bi > 0 strictly, then necessarily Biw* > 0, so if pi* = 0, then necessarily, Biw* - pi* > 0. But then, by condition (6), we must have it that xi* = 0. This can be interpreted as follows: if an output is free (pi* = 0) , then that output will not be produced (xi* = 0). But in equilibrium (1), we have it that zi(p*) = Di(p*, w*) - xi* £ 0. As Di(p*, w*) ³ 0, then it must be that if xi* = 0, then Di(p*, w*) = 0. Thus, in sum, if pi* = 0, then necessarily zi(p*) = 0, i.e. there are no free outputs in equilibrium. This is what (1¢ ) states.§ Let us now turn to one of Wald's major concerns: uniqueness of equilibrium. Wald (1936) introduced the following famous assumption:
This can be interpreted as follows: if D is chosen at price p when D¢ was affordable, then if D¢ is chosen at p¢ , then it must be because D¢ was not affordable at those prices. There are two forms of WARP introduced by Wald: one for the individual demand functions (what he called Condition 6w) and one for the market demand functions (what he called Condition 6). However, Wald was careful enough to remind us that these are two different conditions: WARP at the individual level does not imply and is not implied by WARP at the market level (as later confirmed by the Debreu-Sonnenschein-Mantel theorem). However, he writes that "there is a statistical probability that, from the assumption that (6w) holds for every [household], the validity of (6) follows" (Wald, 1936a:p.292), but he did not prove this. We should note that Wald (1936b) does go on to prove that WARP will be satisfied if we impose the assumption that all goods are gross substitutes -- a result later much used in stability theory during the 1950s and 1960s. The proof of uniqueness on the basis of WARP is quite simple. Let p* and p** represent two distinct equilibrium price vectors, thus by definition, z* = D* - x* = 0 and z** = D** - x** = 0. Now, we claimed that D** was feasible when prices were p*, thus x** was feasible in the linear program generated by p*, i.e. in max p*x s.t. v ³ B¢ x. But since x* is the solution to that program, then necessarily p*x* ³ p*x**, where we have it that v ³ B¢ x* and v ³ B¢ x** (both x* and x** are feasible). However, when x** chosen in its own program, max p**x s.t. v ³ B¢ x, notice that the constraints have not changed from the previous program. In other words as v ³ B¢ x*, then x* must be feasible in the second program. Consequently, as x** is the optimal solution, we obtain p**x** ³ p**x*. But this is a clear violation of WARP: x* was chosen when x** was feasible, and x** was chosen when x* was feasible. Thus if WARP holds, then it must be that p* = p** and x* = x**, i.e. the equilibrium is unique. (5) The Wald System with Capital We can easily add intermediate goods into the Wald construction, exactly as we did before for the Walras-Cassel model. Let A be a matrix of unit output demands for intermediate goods (i.e. produced factors) and B a matrix of unit output demands for primary factors. Thus, the market-clearing condition for produced goods is now:
i.e. output supplies (x) must equal input demands (Ax) and consumer demands (D(p,w)). In contrast the market-clearing condition for primary factors remains:
i.e. supply of primary factors is equal to the demand for primary factors. In contrast, the price-cost inequalities now include the following:
where Ap is the cost of intermediate goods and Bw is the cost of primary factors. As a result, the primal program of the Wald model can be rewritten as:
while the dual is:
By redefining prices as net prices, i.e. p° = (I - A)p, our price-cost inequalities become p° £ Bw and by re-expressing our outputs as net outputs, x° = (I - A)x, thus we now have x° = D(p, w) as our output market-clearing condition. As a result, we can rewrite the primal and dual problems as:
which is effectively the same as in the old Wald system, only now with adjusted prices. In contrast the dual is:
which is, again, identical to the old Wald system, except with adjusted prices p0. The solution then proceeds as in the conventional Wald model. For more details, refer to our earlier references on capital and growth in the Walras-Cassel model. W.J. Baumol and S.M. Goldfeld (1968) Percursors of Mathematical Economics: An anthology. London: London School of Economics. R. Dorfman, P.A. Samuelson and R.M. Solow (1958) Linear Programming and Economic Analysis. New York: McGraw-Hill. D. Gale (1960) The Theory of Linear Economic Models. New York: McGraw-Hill. L. Kantorovich (1959) The Best Use of Economic Resources. 1962 translation, Oxford: Pergamon. S. Karlin (1959) Mathematical Methods and Theory in Games, Programming and Economics, Vol. I & II. Reprint, New York: Dover. H.W. Kuhn (1956) "On a Theorem by Wald", in H.W. Kuhn and A.W. Tucker, editors, Linear Inequalities and Related Systems. Princeton: Princeton University Press. R.E. Kuenne (1963) The Theory of General Economic Equilibrium. Princeton: Princeton University Press. K.J. Lancaster (1968) Mathematical Economics. 1987 reprint, New York: Dover. H. Neisser (1932) "Lohnhöle und Beschäftigungsgrad in Marktgleichgewicht", Weltwirtschaftliches Archiv, Vol. 36, p.413-55. K. Schlesinger (1935) "On the Production Equations of Economic Value Theory", in Menger, editor, Ergebnisse eines mathematischen Kolloquiums, 1933-34. Translated and reprinted in Baumol and Goldfeld, 1968. H.F. v. Stackelberg (1933) "Zwei kritische Bemerkungen zur Preistheorie Gustav Cassel", Zeitschrift für Nationalökonomie, Vol. 4, p.456-72. A. Takayama (1974) Mathematical Economics. 1985 (2nd) edition, Cambridge, UK: Cambridge University Press. A. Wald (1935) "On the Unique Non-Negative Solvability of the New Production Functions (Part I)", in Menger, editor, Ergebnisse eines mathematischen Kolloquiums, 1934-35. As translated and reprinted in Baumol and Goldfeld,1968. A. Wald (1936) "On the Production Equations of Economic Value Theory (Part 2)", in Menger, editor, Ergebnisse eines mathematischen Kolloquiums, 1934-35. As translated and reprinted in Baumol and Goldfeld, 1968. A. Wald. (1936) "On Some Systems of Equations of Mathematical Economics", Zeitschrift für Nationalökonomie, Vol.7. Translated, 1951, Econometrica, Vol.19 (4), p.368-403. E. R. Weintraub (1983) "The Existence of Competitive Equilibrium: 1930-1954", Journal of Economic Literature, Vol. , p.1-39. ________________________________________________________
|
All rights reserved, Gonçalo L. Fonseca