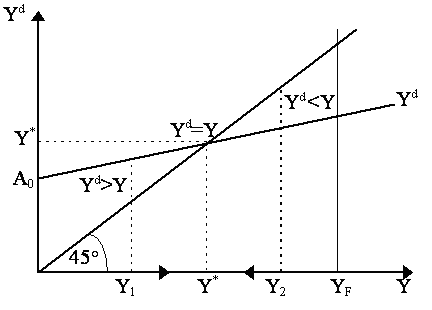|
Roy Harrod (1937), James Meade (1937) and Oskar Lange (1938) had attempted to express the main relationships of Keynes's theory as equations in order to elucidate the interrelationships between the theory of effective demand and the theory of liquidity preference. In a similar effort, John Hicks, in his famous 1937 Econometrica article, "Mr Keynes and the Classics: A suggested interpretation", drew two curves, "SI-LL" to illustrate these relationships. These curves have since become famously known as the IS-LM model and were popularized by a now-converted Alvin Hansen (1949, 1953). The IS-LM model has remained one of the most formidable pieces of pedagogic machinery and, as far as back-of-the-envelope diagrammatic reasoning is concerned, one of the most efficient ever devised in economics. It is not, however, without substantial problems, both as an internally consistent model or as a representation of Keynes's theory. The crucial feature of the Keynesian system Hicks and Hansen concentrated on when formulating the simple IS-LM is the interaction between the real and monetary markets. From the real market, one extracts the level of income (Y) and from the money market, one obtains the interest rate (r). These variables, in turn, affect elements in the other market - in the simplest version, income affects money demand and interest affects investment. This interaction clearly violates the "classical dichotomy" and, as we shall see, it also does not support the neutrality of money. Financial-real interaction is the core of the IS-LM version of Keynes's theory - therefore, Hicks (1937) concluded with perfect Walrasian instincts, it is necessary to solve for the money and real markets simultaneously. However, many Keynesians, such as Pasinetti (1974), have argued that Keynes's system should be thought of "block recursively" or "sequentially" and thus should not be solved simultaneously. Specifically, it can be argued that the Keynesian system ought to be seen as a sequence of alternating "asset market" and "goods market" decisions - the interest rate being first determined by a portfolio decision in the financial markets and only thereafter determining investment, output and employment in the real market which then feeds back into another portfolio decision, etc. This criticism is noteworthy because the portfolio (LM) decision is made in the context of a stock constraint whereas the real market decisions (IS) is made in a flow constraint. Furthermore, as Richard Kahn (1984) and Joan Robinson (1973, 1978, 1979) emphasized later, the simultaneous equation method of the IS-LM, by eliminating sequential time, also eliminates the time-dependent concepts which they saw as fundamental to Keynes's theory - such as uncertainty, expectations, speculation and animal spirits. As John Hicks (1980, 1988) himself notes in his recantation, these different time references for IS and LM makes the simultaneous IS-LM model incongruous (see also Leijonhufvud, 1968, 1983; Davidson, 1992). The following construction of the IS-LM ignores these problems and is built on the original Hicks-Hansen presentations. The best place to begin is perhaps the very familiar income-expenditure diagram - the "Keynesian cross" - which Paul Samuelson (1948), Abba Lerner (1951) and Alvin Hansen (1953) made popular. Let total planned expenditures - i.e. "aggregate demand" - be:
where C is planned consumption, I is planned investment and G is planned government spending (and we are ignoring the foreign sector). It is true at all times that actual aggregate expenditure equals aggregate supply (and total income). But it is possible for planned expenditures in a period to exceed or fall below output - the difference being made up by changes in inventories (previously-produced output in storage). So, defining Y as total current output, then it is certainly possible for aggregate expenditures to exceed current output (Yd > Y), the extra sales being made up by drawing prior output from inventory. Similarly, if Yd < Y, then then the unsold excess is added to inventory. But here is the critical bit of the Keynesian story: firms will react and adjust output in response. You can think of it as firms trying to maintain a roughly stable inventory and take changes in inventory as indicators of when to increase or decrease supply. A firm which finds its inventory quickly depleting will increase its production orders for the next period, thereby output will increase. A firm which finds its inventories accumulating unsold, will scale back its orders for output next period, thus output falls. Summarized:
These are the fundamental Keynesian output dynamics. Output (aggregate supply) adjust to expenditures (aggregate demand): Excess demand and supply in the goods market is met by output adjustments. If there is goods-market equilibrium, then aggregate demand must equal aggregate supply:
As people are paid to produce output, then by definition, total output is identical to total income. Now, income is either consumed, saved or taxed away, thus we can decompose Y into:
where the terms follow their traditional definitions (S is savings, T is taxes). Consequently, at goods market equilibrium (Yd = Y): C + I + G = C + S + T or, simply, assuming a balanced government budget (so G = T), then the equilibrium condition Yd = Y can be written equivalently as:
thus planned investment equals planned savings. The equilibrium level of output is potentially any level up to the full employment level. Which level of output actually happens to be the equilibrium depends entirely upon aggregate demand - hence aggregate demand is the primary determinant of the equilibrium level of output. This is indisputably the central message of Keynes's theory. Given any level of aggregate demand, producers will try to meet that demand and thus aggregate output will rise or fall to equate the given aggregate demand. There is the nub, of course, that aggregate demand is itself dependent on income. This is principally because consumption, one of the main components of aggregate demand, depends on income. This may, on first glance, seem circular in reasoning - aggregate demand determines output, but we cannot determine aggregate demand without knowing what output is first. But of course, it is not circular, but an issue of mathematical simultaneity. Dynamically, output at a given time determines aggregate demand, which may exceed it or fall below it, and set in motion changes in output as outlined above. It is in the final instance, when output produces the aggregate demand that matches that output, that we are in a stable, equilibrium situation. This is what is captured by the "Keynesian cross" diagram (Fig. 1), plotting expenditures against output. Because of the consumption relationship, the aggregate demand function (Yd) depends on income (Y). The 45° line simply bounces the level of Y. If income is Y1, then the aggregate demand generated exceeds the output which generated it (i.e. Yd > Y wherever the aggregate demand line is above the 45° line). But as we know from the Keynesian dynamics outlined above, such a situation is unstable - output will rise in response. So output will not stay at Y1 but increase, moving right towards Y*. If income is Y2, then the aggregate demand generated is less than the output which generated it (i.e. Yd < Y, aggregate demand line is below the 45° line). This situation is also unstable, output will fall, moving left towards Y*. It is only at Y* where aggregate demand generated matches the output that generated it (i.e. aggregate demand intersects the 45° line) that output will remain stable and unchanged. This level of output may or may not match the full employment level of output. In Figure 1, the equilibrium level of output (Y*) is below full employment output (YF). There are no mechanisms here that push it towards it. The dynamics push all output levels towards Y*. Thus the Keynesian cross model is the simplest, first approximation to the Keynesian idea that total output in an economy can settle at an equilibrium below full employment.
The computation of the equilibrium output level Y* is actually a quite simple result of the Kahn-Keynes "multiplier". Letting consumption be a linear function of current income:
where c is the marginal propensity to consume (MPC) so 0 < c < 1, and C0 is autonomous consumption. Assuming, in turn, that investment demand and government spending are exogenous, (i.e. I = I0 and G = G0), then aggregate demand becomes:
which is shown in Figure 1 as the aggregate demand function, Yd. Note that the slope of this curve is the marginal propensity to consume (c) and because 0 < c < 1, the aggregate demand function Yd is flatter than the 45° line. The vertical intercept is merely the collection of autonomous terms, A0 = [C0 + I0 + G0]. Obviously, in equilibrium, it must be that Y = Yd. Thus, solving for equilibrium output, Y*:
so the equilibrium level of output is some multiple of the autonomous terms (C0 + I0 + G0), where the term 1/(1-c) is the Kahn-Keynes "multiplier". The equilibrium level of output, Y*, is shown in Figure 1 as the point where the aggregate demand function intersects the 45° line. The basic reasoning behind the Kahn-Keynes multiplier is the idea that expenditure (by people, firms or government) will generate income for somebody and that subsequently some of this income will be consumed and thus generate more expenditure which will in turn generate more income and thus more expenditure, etc. Thus, if autonomous expenditure is C0+I0+G0, then this will be someone's income; thus consumption increases by c(C0+I0+G0), which, in turn, is also an increase in someone's income and thus consumption increases again by c(c(C0+I0+G0), and so on through successive rounds. Thus, the total income generated by an initial autonomous level of expenditure C0 + I0 + G0 will be:
or factoring out c:
However, this geometric progression is not eternal: this is a convergent series because the marginal propensity to consume is a fraction. In other words, if 0 < c < 1, then the sum of an infinite geometric progression (1 + c + c2 + c3 + ....), can be approximated by the expression 1⁄ (1-c). Thus:
As the term 1/(1-c) > 1, it is commonly known as "the multiplier". The initial autonomous expenditures [C0 + I0 + G0] have generated (1⁄ (1-c)) [C0+I0+G0] of income in the economy as a whole after the multiplier process works itself out. Naturally, there is also a disequilibrium dynamic underlying the system implied the Kahn-Keynes "multiplier" process explained above. Specifically, the dynamic of the multiplier argues that output responds to excess demand for goods:
where ¦ ¢ > 0, so output increases if there is excess demand for goods (Yd > Y or I > S) and output decreases if there is excess supply of goods (Yd < Y or I < S). This is very different from the Neoclassical macromodel which argued that it was interest rates that cleared the goods market. Now, we noted earlier, following Lerner (1938, 1939, 1944), that actual savings always equals actual investment, thus we must remind ourselves that the I and S denoted here refer only to planned levels of investment and savings. To see why, assume that output is at a position to the left of Y* in Figure 1, such as Y1. At this point, output Y1 is given, thus, by extension, S is fixed. However, obviously, at this point, aggregate demand exceeds aggregate supply, Yd > Y (equivalent to I > S). How can Lerner be correct? Easily. Note that as there is excess demand for goods thus there must be unplanned depletion of firms' inventories - which implies, in turn, that there is unplanned disinvestment. This unplanned disinvestment is the difference between planned investment and planned savings - i.e. the interval at Y1 between the two curves, Yd and the 45° line. Thus, although planned investment exceeds planned savings, actual investment (planned investment minus unplanned disinvestment) is equal to actual savings. The multiplier dynamic, then, proposes that as firms see their inventories deplete unexpectedly, they take this as a signal of excess demand for their goods and consequently increase production - thereby raising output back up to Y*. We can see the same thing for the other side: suppose actual output is to the right of Y*, for instance, at Y2 in Figure 1. In this case, Yd < Y or planned I is less than planned S - or, quite simply, there is unplanned inventory investment as excess goods supply accumulate on inventory shelves. Firms take this as a signal to cut back output - and therefore Y is reduced to Y*. Thus, the Keynesian multiplier dynamic implies that output (Y) does all the adjusting in response to disequilibrium in the goods markets. [Alternatively, the interim difference between aggregate demand and supply can be regarded as representing unplanned or forced savings and dissavings rather than unplanned inventory decumulation and accumulation respectively. Such a characterization, reminiscent of the earlier Wicksellian literature (e.g. Hayek, 1931), would imply that it is consumers expenditure plans, and not necessarily those of firms, which are contradicted in disequilbrium. The resulting multiplier dynamic would not be affected by such an interpretation, although it may seem less natural.] We have noted that we can determine the equilibrium level of output, Y* once we know what the marginal propensity to consume (c) is and what the autonomous terms C0, I0 and G0 are. However, this is a heavily stripped version of the model and these terms ought to be a bit more detailed. For instance, consumption can be defined as:
where C0 is autonomous consumption, c is the marginal propensity to consume out of current disposable income, where disposable income is defined as actual income Y minus taxes, TX, which in turn, can be defined as TX = TX0 - TR0 + tY where TX0 are autonomous taxes (e.g. excise taxes), TR0 are net government transfer payments (e.g. unemployment benefits) and t (where 0 < t < 1) is the marginal tax rate so that tY reflects income taxes. In this case, consumption becomes:
which is a bit richer than our earlier expression for the consumption function. The more interesting change in the model is in the description of the investment demand function. Specifically, assume that investment is a negative function of interest rates, r, so that investment demand becomes:
where Ir < 0 and I0 is autonomous investment. Note that, written thus, investment is a negative function of only one interest rate - this is already a Hicksian modification of the original story. Continuing to assume that G = G0 is completely autonomous, total planned expenditures are now:
Thus, in equilibrium, Y = Yd and thus solving for equilibrium output Y*:
or letting A0 denote all the autonomous terms, i.e. A0 = [C0 + c(TR0 - TX0) + I0 + G0 + I(r)], which will be the intercept of our Yd curve, then it follows that:
where 1/(1-c(1-t)) is the new multiplier. Of course, 0 < (1-c(1-t)) < 1 thus the aggregate demand function has still a flatter slope than the 45° line, thus there will be an intersection which will yield us equilibrium Y*. We could have made this richer by adding a foreign sector and thereby including autonomous export/import terms and a marginal propensity to import into the multiplier term, but the lesson we believe is clear at this point: whatever we wish to include in the set of autonomous terms or into the multiplier in order to increase "realism", there is an equilibrium level of output Y* that is determinate and a multiplier dynamic that ensures that it is stable. The most important result of this exercise is that Y* corresponds to an equilibrium output level, where I = S, but which may or may not imply full employment. Y* is just one of a continuum of possible output levels. In Figure 1, full employment is noted by YF which is definitely higher than Y* but, contrary to the Neoclassical model, there are no inherent mechanisms to drive the equilibrium level of output to the full employment level. The economy will therefore be sustained at an "underemployment equilibrium". Furthermore, note that any changes in any of the autonomous terms (e.g. C0, TX0, TR0, I0, I(r), G0) will lead to a change in A0 and consequently a change in the intercept of the Yd line - and consequently the resulting equilibrium level of output, Y*. It is thus easy to visualize that fiscal policy variables, such as government spending (G0), autonomous taxes (TX0), government transfers (TR0) or (via a slightly different channel) the income tax rate (t) will affect the equilibrium level of output, Y*. Thus, equilibrium is policy-effective: government can, by means of increasing spending and transfers or reducing taxes, increase the equilibrium level of output Y*. Thus, Keynesian propositions about the government using expenditure and tax policy to assist the economy by pushing equilibrium output Y* to the full employment level YF - part of what Abba Lerner (1943, 1944) called "functional finance" - are obvious here. Naturally, government fiscal policy variables are not the only things included in the intercept A0: autonomous consumption (C0) and investment terms (I0, I(r)) also affect the equilibrium level of output. Keynes was particularly interested in investment - "that flighty bird" - and how it helped determine the equilibrium level of output and how that could be changed. Specifically, note that investment is a function of the interest rate, r - thus our model is not exactly "closed" because we have said nothing about how the interest rate, r, is determined. Now, the relationship between interest and investment is via the "marginal efficiency of investment" or MEI - as Lerner (1944) appropriately rebaptized it. Essentially, we can think of the MEI curve as downward-sloping: as investment increases, the marginal efficiency of investment collapses. Firms, Keynes proposed, will invest until the MEI is equal to a given rate of interest. Thus, the lower the rate of interest, the greater the amount of investment and vice-versa, thus I(r) is such that dI/dr < 0. Thus, we can begin to set out Hicks's "IS" curve - the equilibrium locus which captures the relationship between interest rate and output. As interest rate rises, I(r) falls and consequently so does Yd - thus, the equilibrium level of output, Y* declines. Thus, as we see in the Figure 3, the IS curve is downward sloping: high r is related with low equilibrium output Y* while low r is related with high Y*. This is an equilibrium locus and not a curve - any point on the curve represent goods market equilibrium, where aggregate demand equals aggregate supply. Points off the curve represent disequilibrium points. For instance, at a given r, we obtain a particular Y* so that if output is actually greater than Y* (Y > Y*) the multiplier dynamic implies that it must fall towards the locus. Similarly, if Y < Y* at a given r, then output must rise towards Y* and thus towards the locus. Thus, points to the left of the IS curve represent points where there is "excess demand" for goods whereas points to the right of the IS curve situations of "excess supply" of goods. The horizontal directional arrows shown in Figure 3 summarize the multiplier dynamic. We can immediately see that a rise in government spending (G), a rise in transfers (TR0), a decline in taxes (TX0, t), an increase in autonomous investment (I0) or an increase in autonomous consumption (C0) or the propensity to consume (c) all lead to a rightward shift in the IS curve. The opposite cases imply a leftward shift. Now, given:
then by totally differentiation with respect to r and Y, we can note that
denotes the slope of the IS curve. Thus the lower the income sensitivity of expenditure (the lower the marginal propensity to consume and the higher the income tax rate) and the lower the interest sensitivity of investment, then the steeper the IS curve. Conversely, a high income sensitivity (i.e. a high multiplier) and a high interest sensitivity of investment imply a flatter IS curve. However, we have still to determine the rate of interest - this is where Keynes's theory of liquidity preference comes in. As he writes:
What this means is that people possess a portfolio of assets for which they try to find the "right" liquidity mix. For simplicity, it is assumed to contain only two assets: money (which yields nothing but is highly liquid) and "bonds" (which yield interest but are illiquid). If the rate of interest were zero, nobody would hold bonds in their portfolios - for the liquidity provided by the money would be far superior. However, in order to convince people to "part from liquidity", bonds offer a rate of interest. The greater the rate of interest, the greater the enticement to move away from money and hold bonds instead. Although the issue of expected and actual rates of interest (and a multiplicity of these) is an issue that was papered over by Hicks (1937), the gist of the story can be captured by recognizing that money demand can be written:
where Lr < 0 and LY > 0, thus as interest rate rises, the demand for money falls (as people prefer to buy interest-bearing bonds) while as output rises people demand more money (as people need money to conduct more transactions). The dependence of money demand on income is a crucial relation - originally mentioned but suppressed by Keynes, and then resurrected by Hicks and Hansen. In contrast, the supply of money is written as:
where M is the nominal money supply which is regarded as exogenously determined and the price level, p, for the moment will be left unexplained. For money market equilibrium, then Md = Ms, or:
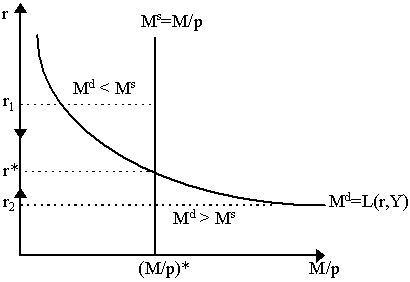
The money market equilibrium is shown in Figure 2.
Obviously, the interest rate brings the money market into equilibrium, but how is that possible? We learn in regular microeconomics that the market for apples is cleared by the price of apples - how then is the market for money cleared by the price on another good, i.e. bonds? To understand this, let us note that Keynes implied was the existence of a portfolio stock constraint, which can heuristically be set out as follows:
where the total demand for wealth is Md + Bd and the total supply of wealth is Ms + Ms. By assuming Walras's Law for stocks, a crucial assumption, then this equation will hold true at all times. Now, Keynes claimed that the rate of interest is determined by the supply and demand for bonds. But if interest rate clears the bond market (so Bd = Bs) then we see that necessarily Md = Ms, the money market clears - thus we can also say (as Keynes did repeatedly) that interest rates are determined by the supply and demand for money. In view of the Walras's Law stock constraint, bond market equilibrium and money market equilibrium are, indeed, one and the same thing. If interest rates are too high so that bond demand exceeds bond supply (Bd > Bs), we can see that, via this stock constraint, this translates necessarily into Md < Ms, i.e. an excess supply of money. We can see how this is depicted in Figure 2 when we consider r1 > r*. The portfolio dynamics are simple supply-and-demand logic: if there is excess demand for bonds, then the price of bonds will rise, which means that the rate of interest on bonds will fall - thus r1 declines towards r*. Similarly, the opposite case is also true: when interest is below r* (at, say, r2), then bond supply exceeds bond demand by regular logic - but then, by the stock constraint, this implies that there must be excess demand for money. The dynamics also apply: when there is excess bond supply, then the price of bonds falls and thus the interest rate on bonds rises - so we move from r2 back up to r*. Thus, all this is captured in the money-market diagram alone. Thus, by recognizing this Walras' Law relationship implied by the portfolio allocation of wealth, we can claim that interest rate on bonds is determined in the money market, even though the details of the story are told in the bond market. For more thoughts on this matter, see our review of Keynes's General Theory. Now, recall that Md = L(r, Y), thus money demand is also a function of output, Y. When output rises, the money demand curve will thus rise and therefore the equilibrium level of interest rates, r*, will also rise. Consequently, following Hicks (1937), we can derive an "LM" curve as the equilibrium locus which relates output levels to equilibrium levels of interest. As we see in Figure 3, this is a positive relationship, thus the LM is upward sloping. Keep in mind the important fact that LM represents money market equilibrium, thus M/p = L(r, Y) anywhere along the LM curve. Any point off the LM curve will denote a money-market disequilibrium. Specifically, at a given rate of output, if r is too high, then by the dynamics proposed earlier apply: if r > r*, then there is excess money supply and r declines; whereas if r < r*, then there is excess money demand and r increases. Thus, all points above the LM curve denote situations of excess money supply whereas all points below the LM curve are situations of excess money demand. Thus, the vertical directional arrows in Figure 3 denote the dynamics implied by the financial markets. It is obvious that the LM shifts on the basis of many parameters. An increase in the nominal money supply M, a decrease in prices p, a decrease in the bond supply Bs, an decrease in money demand Md or an increase in bond demand, Bd, all lead to a rightward shift in the LM curve. The opposite of any of these leads to a leftward shift in the LM. Totally differentiating the equilibrium locus:
so as d(M/p) = 0, then, the slope of the LM curve is:
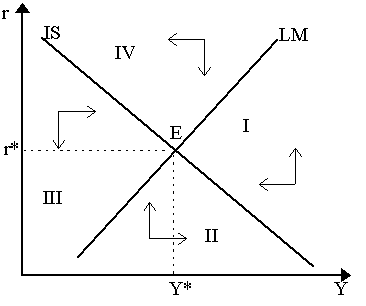
where LY is the income sensitivity of money demand and Lr is the interest sensitivity of money demand. Thus, if LY is high and Lr is low, we get a steep LM curve. If LY is low and Lr high, then we get a very flat LM curve. What Hicks (1937) called the "liquidity trap" assumes an extreme case of the latter. In Figure 3, we superimpose the IS and LM curves to generate the IS-LM diagram. Immediately we can notice that the only point in the diagram where both goods markets and money markets are in equilibrium is at point E, where r = r* and Y = Y*. This is the equilibrium level of output and interest where both goods and money markets clear. By examining the directional arrows implied by the goods market multiplier and the money market financial dynamics, we can notice immediately that equilibrium E is stable as all trajectories tend towards it sooner or later (the IS curve, of course, is nothing but the isokine for dY/dt = 0 and the LM curve being the isokine for dr/dt = 0 - thus the dynamics are easy to derive).
It might be worthwhile reminding ourselves what the disequilibrium quadrants (denoted in Figure 3 by I-IV) imply:
Immediately we can begin seeing some implied problems. As Hicks (1980) later carefully noted, one cannot really superimpose a stock equilibrium over a flow equilibrium because their time references are different. To see this, we must realize that any point on the LM curve implies a stock equilibrium - thus, by definition, the demand for wealth equals the supply of wealth. But recall that planned savings translate into additional demand for wealth while planned investment translate into additional supply of wealth. Consequently, how is it ever logically possible, then, to be on the LM curve but not on the IS curve? In other words, by imposing stock constraint at all times, it can never be that the flow constraint is in disequilibrium - thus planned I = S at all times as well. Other familiar problems re-emerge here: does not Keynes's theory of liquidity preference hinge on at least two interest rates, the future expected rate and the current rate? Where are these? These are just a few of the many difficulties implied by an IS-LM depiction of the Keynesian model. However, as a pedagogic, back-of-the-envelope device, IS-LM is supremely efficient. We can see this mechanically. Increases in autonomous effective demand variables (C0, I0, G0, TR0, -TX0 etc.) all lead to rightward-shifts in the IS curve and consequently a new equilibrium at a higher level of output and interest. Increases in money supply, falls in the general price level, lower money demand, etc. all lead to a rightward shift in the LM curve and thus a higher level of output and lower level of interest. Notice also that the relative efficacy of fiscal policy (via IS) and monetary policy (via LM) depend crucially on the slopes of the IS and LM curves - and thus on the presumed interest and income sensitivities of money demand, investment, consumption and other expenditure categories. A relatively steep LM curve and flat IS curve imply that monetary policy is highly effective whereas the converse case of a relatively flat LM curve and steep IS cure imply that fiscal policy is highly effective. The manifold stories which can be told via the Hicks-Hansen IS-LM diagram almost permits one to overlook the logical and theoretical difficulties that underlie it. However, as is evident in the work of many prominent Keynesian economists - such as Abba Lerner (1944, 1951, 1952), Tibor Scitovsky (1940), Sidney Weintraub (1958, 1959, 1961, 1965) and Paul Davidson (1972, 1994) - who never used this apparatus, the IS-LM model is neither the only, nor the most faithful, nor the most coherent tool in which to express Keynes's General Theory - but it might very well be the simplest.
|
All rights reserved, Gonçalo L. Fonseca