|
________________________________________________________
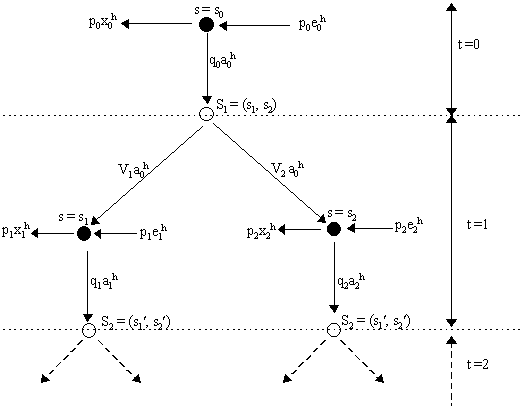
Notation The Arrow-Debreu economy - as set out by Arrow (1953) and Debreu (1959) - is an intertemporal, perfect foresight world with a complete set of future state-contingent markets available at the initial time period. Thus, the only thing an agent has to do is to purchase a set of future state-contingent commodities in the initial time period and then just watch the future unfold. A state-contingent commodity, recall, is a contract that promises to deliver to the holder of that contract a particular commodity when a particular state occurs at a particular time (and delivers nothing at any other state and/or time). Thus, a "commodity" in the Arrow-Debreu world is a good which is described by its physical properties, its location in time, and the state of the world in which it is delivered, e.g. "eggs delivered on June 2, 2001 if it is sunny". Assuming there are n types of physically-differentiated goods, S possible states of nature every period and T time periods, then we need nST markets open at the initial time period. Requiring that such a large set of future and state-contingent markets be open at once is a difficult thing to accept. Economists owe it to Kenneth J. Arrow (1953) the realization that we do not really need a full set of commodity-specific state-contingent contracts to obtain the Arrow-Debreu equilibrium. Arrow's insight was to argue that financial securities perform this function as well. As an example, he proposed a sort of security which promises to pay a unit of a numeraire good if a particular state in a particular time period occurs and nothing otherwise - what has since become known as an "Arrow security". What Arrow argued is that if we wish to consume eggs and bacon on June 2, 2001, we do not need to purchase a contract which delivers eggs at that state and time and a contract which delivers bacon at that state and time. Instead, we only need to purchase a contract which yields money (or some unit of account) on June 2, 2001 which we can then use to purchase eggs and bacon on the spot market. As a consequence, Arrow argued that in order to transfer purchasing power across all states, we really only need a single "Arrow security" for each state of nature. Thus, if we have S possible states in any time period and n physically-differentiated commodities, we merely necessitate S securities for each time period rather than nS. Thus, in the initial time period, we only need (n+s)T markets to exist - as opposed to nST state-contingent markets - in order for agents to carry out their intertemporal consumption plans. However, there is one substantial modification to the Arrow-Debreu scenario required if we adopt this suggestion: namely, we must allow spot markets to be open in the future. Recall that with the Arrow-Debreu scenario, agents make a perfect-foresight decision on their consumption patterns from the outset and then purchase and sell intertemporal and state-contingent contracts at the initial time period. As these contracts are presumed to remain binding, then markets do not need to remain open once all contracts are made in the initial time period. Thus, in the Arrow-Debreu world, markets only open once, at t = 0, and will never open again as time progresses (and, even if they did, there would be no trading as the equilibrium in future state-contingent markets implies Pareto-optimality and thus no mutually beneficial trades are possible). However, adopting the Arrow securities approach, when the full set of future state-contingent markets replaced by a far fewer set of markets for financial securities, markets cannot close after the initial trading day. Trading must occur in the future: when agents securities are liquidated into purchasing power, agents will use the proceeds to purchase goods on the spot markets at that time period. Commodity markets must, therefore, be open in every time period. Thus, the intertemporal Arrow-Debreu economy is replaced with a "sequential" economy. The idea of a sequential economy has an old history. In a general equilibrium context, it had been pursued by John Hicks (1939) and the Stockholm School theorists (Erik Lindahl (1939) and Erik Lundberg (1937)). In a sequence economy, instead of one great competitive equilibrium determined at an initial moment which then remains binding for all time, the sequence economy considers a sequence of equilibria. In simpler jargon, the "long run" general equilibrium is viewed merely as an interlinked succession of "short run" equilibria. In the Hicks-Lindahl sequential scenario, consumption pattern decisions are made, but either binding intertemporal or state-contingent contracts are not fully available and/or foresight is not perfect. Thus, agents make a consumption plan based on expectations of future prices of commodities, and then purchase two types of objects: goods (to consume now) and assets (to carry purchasing power over to future periods when they can be traded for consumption goods). Markets open at t = 0, but they also open at t=1 and t = 2, etc. as traders buy and sell assets and commodities time and time again. Thus, successive "Hicksian weeks" (spot product markets) are interlinked with each other via asset markets. The Hicks-Lindahl theory remained dormant for a long time. The introduction of sequential economies into modern general equilibrium theory arose from difficulties arising in integrating the theory of money into Walrasian theory -- as highlighted by the seminal critique of Frank H. Hahn (1965). Hahn identified the basic difficulty: namely, in a perfect foresight, finite-dimensional Walrasian scenario, money had no essential purpose. If a full set of future state-contingent contracts are available, then why should agents demand money? The first step in the process of integrating money into general equilibrium theory was to assume, therefore, that a full set of contracts was not available. In this case, as outlined above, a role for financial assets (such as money) emerges - but, as we saw, that necessitates a sequential structure. We can think of a sequential economy as a succession of time periods each with its own set of states, as shown heuristically by the schema in Figure 1. At t = 0, we are at the initial state, s0, which is certain. Trading then occurs in (spot) commodity markets and asset markets. Anticipating our notation, let e0h be the endowment of the hth household in the initial time period. Let p0 be the set of commodity prices and q0 the set of asset prices in the initial time period. Households subsequently purchase consumer goods for consumption now (bundle x0h which will cost p0x0h at the current spot prices) and a portfolio of assets to transfer purchasing power to t = 1 (portfolio a0h, which will cost q0a0h at current asset prices). They must make these purchases with the concurrent sale of endowments, thus agent h has a budget constraint at time t = 0 that looks like p0x0h + q0a0h £ p0e0h. Now, at t = 1, there may be several states of the world which emerge. This is shown in Figure 1 to be S1 = (s1, s2). At this node, Nature plays its role and chooses a particular state - either s1 or s2 will be true. As endowments are random, the households receive different endowments in different states, esh, where s Î (s1, s2). Similarly, assets purchased in the previous period t = 0 yield different returns in different states, thus we denote Vsa0h the return to asset portfolio a0h if a particular state s Î (s1, s2) occurs. Thus, household "income" in any state s in period t = 1 will be psesh + Vsa0h where ps is the spot price vector in state s. They use this income, of course, to purchase commodities again (bundle xsh which costs psxsh at the prevailing spot prices in state s) and another set of assets, ash to transfer purchasing power to the next period, t = 2 (portfolio ash which costs qsash at the prevailing asset prices in state s, which we denote qs). Consequently, in a particular state s Î (s1, s2), households face the budget constraint psxsh + qsash £ psesh + Vsa0h. As time progresses and we move to a new time period, t = 2, then we have a new set of states S2 = (s1˘ , s2˘ ) that are possible where, once again, Nature makes the choice and the whole process repeats itself and so on for future time periods and states until the end of time.
Since the flurry of activity in the early 1970s, there have emerged essentially three types of sequential equilibrium: "temporary" equilibrium, "Radner" equilibrium and "rational expectations" equilibrium. They all possess the product markets/asset markets sequential structure outlined above in Figure 1. The essential distinctions between these theories lie in the form of expectations assumed. In short, temporary equilibrium does not require perfect foresight nor information-consistency across agents; Radner equilibrium requires perfect foresight but not consistency; rational expectations equilibrium require information-consistent expectations. "Temporary equilibrium" is the closest to John Hicks's (1939) original vision and has cropped up since in various forms before being analyzed rigorously by Bent Stigum (1969) and Jean-Michel Grandmont (1974, 1977). In temporary equilibrium, agents form ex ante expectations of prices in future spot markets and make the sort of sequential product market-asset market decision shown schematically in Figure 1: deciding which current goods to consume and produce now and how many financial assets to buy/sell in order to bring purchasing power into/from the future in anticipation of buying a particular basket of commodities then. However, in "temporary equilibrium", there is no requirement that these ex ante expectations be fulfilled: spot markets for both commodities and assets clear within the "Hicksian week" on the basis of current demands and expectations of future spot prices, but these expectations may very well be different from the actual spot prices that emerge in the future. What we have, then, is a sequence of spot-market "temporary" equilibria with expectations being contradicted or fulfilled in every successive week. As Lindahl described it many years before:
In contrast, Roy Radner (1972) laid out an equilibrium of "plans, prices and price expectations". This also possessed a sequential structure, but he required perfect foresight as well. In other words, spot markets are required to clear every period as before, but it is also required that the spot prices that emerge in the future be consistent with current expectations. In Radner's model, then, markets remain open over time, but the trading that occurs in them does not yield unexpected prices. One of the more interesting results of the Radner equilibrium is that we can replicate the result of an Arrow-Debreu economy. Specifically, consumption plans are made as if we are in an Arrow-Debreu economy: the trading that occurs in the future in the Radner economy can be thought of as sequential analogue of the carrying out of contracts settled upon in the initial period in the Arrow-Debreu economy. The main point, then, is that an Arrow-Debreu equilibrium is replicated without requiring a full set of contingent markets at the initial time period but rather only a set of markets and a sequence of open goods markets. A Radner equilibrium can be visualized as follows: agents form expectations of spot prices in future states, purchase present goods and securities on the basis of those expectations. Current and future spot prices of goods and assets adjust so that all "markets" clear and these price expectations must be fulfilled. As noted, this Radner equilibrium - which is sometimes referred to as a "spot-financial market" equilibrium or a "perfect foresight" equilibrium - is different in detail from the Arrow-Debreu "contingent market" equilibrium" outlined earlier, but it is nonetheless identical in outcome. It is important to come clear as to what this perfect foresight assumption implies. Agents have perfect foresight in the sense that agents "know" which spot prices will emerge if a particular future state occurs.. However, this does not say that agents know which state is gong to actually occur in the future (if we were to make this assumption, then there would be no uncertainty at all and all this apparatus would be irrelevant). Naturally, agents may think some states are likelier to occur than others and thus may form probability assignments over future states. However, an important feature of Radner equilibrium is that these probability assignments are entirely subjective and need not be the same across agents. Differences in belief are not ruled out by the perfect foresight assumption. The only thing perfect foresight assumes is that all agents know which spot prices will occur if state s happens and which spot prices occur if state s˘ happens, but it is perfectly acceptable that a particular agent may think state s is more likely than s˘ and another agent may think s˘ is more likely than s. This brings us to our final type of sequential equilibrium -- the "rational expectations" (RE) equilibrium, which was initially proposed by Lindahl (1939). In the modern context, the concept was introduced by Roy Radner (1967) and made famous by Robert E. Lucas (1972) and Jerry R. Green (1973). A rational expectations equilibrium can be thought of as the special case of the Radner equilibrium when the probabilities assigned by all agents about future states are the same across agents. More specifically, agents are assumed to form "information-consistent" probability assignments. As long as agents have the same information about the future economy (to be specified more formally later), then their probability assignments will be the same. One of the more interesting aspects of this research program is how information is diffused and shared so that we obtain rational expectations. For instance, even if agents begin with different information, a less-informed agent may nonetheless acquire the information the others have by carefully observing the price movements and making inferences from that. Thus, although the "common information" assumption of rational expectations equilibrium is more restrictive than in Radner equilibrium, it can nonetheless be more interesting in that it takes explicit account of the informational role of prices. Finally, we should make note of the burgeoning literature on "incomplete markets" that has emerged in this context -- particularly after Oliver D. Hart's (1975) classical conundrums. The basic idea of incomplete markets, is that we might have a sequential economy where there are an insufficient number of financial securities - specifically, markets are said to be "incomplete" if the number of (linearly independent) securities is strictly less than the number of possible future states. In this case, not all transfers of purchasing power across states are possible. As first discussed by Peter Diamond (1967), the implications of this seem clear enough: agents cannot generally fulfill their optimal intertemporal consumption plan but must make do with a less desirable plan. We can still obtain an equilibrium in "plans, prices and price-expectations" a la Radner, but it no longer true that the resulting outcome is the same as in a contingent market Arrow-Debreu equilibrium. One element that remains somewhat obscure in the sequence economy literature is the issue of why markets may be missing. There are three important aspects to this question: (1) what has eliminated future state-contingent commodity markets in the first place? (2) how do asset markets emerge to replace absent state-contingent markets? (3) (for incomplete markets) why might the resulting asset markets still fail to span the state-returns space? Appeals have been made to some form of transactions costs, bounded rationality, asymmetric information or some combination of these factors. Although any of these assumptions can eliminate a handful of markets and thus force one away from full set of Arrow-Debreu contingent markets, they are external and, in some ways, rather arbitrary. For instance, Frank H. Hahn (1971, 1973) appealed to the existence of transactions costs to explain why some future state-contingent contracts might not be available - or, rather, argued that because using money has lower transaction costs than writing out the relevant state-contingent contracts, then the economy would become organized along sequential lines rather than intertemporal ones. However, it is not difficult to dispute this transactions costs assumption. Alternatively, asymmetric information has been very powerful in explaining the absence of a particular market in partial equilibrium analysis, but it lacks an acceptable generalization to multi-market situations such as the ones we are dealing with here. The great lacunae in the sequential economy literature remains precisely the "micro" explanation of market structure in general and asset structure in particular. To this end, recent work on production and financial decision-making by firms (e.g. Grossman and Hart, 1979) and, in particular, theories of optimal asset structure and financial innovation (e.g. Allen and Gale, 1994) in a sequential multi-market economy, have moved us closer towards addressing these issues and remain active areas of current research. There are many reviews of general equilibrium under uncertainty with such sequential structures. Good general surveys of Radner equilibrium with complete and incomplete markets are found in Radner (1982), Laffont (1989), Magill and Shafer (1991) and, especially, the excellent treatise of Magill and Quinzii (1996). Although concentrating primarily on finance, Duffie (1992) is very much worthwhile consulting in this connection. Temporary equilibrium is reviewed by Grandmont (1977, 1982, 1983). Rational expectations equilibrium is also surveyed in Radner (1982); see also Grossman (1981), Jordan and Radner (1982), Allen (1986) and Bray (1986).
|
All rights reserved, Gonçalo L. Fonseca