|
The raison d'etre of a Radner sequence economy is the absence of a full Arrow-Debreu set of state-contingent markets. Instead, agents transfer purchasing power from t = 0 to t=1 via assets of some sort and then collect (or pay) the payoffs from these assets in the state that actually emerges, and consequently use the proceeds of the sale to purchase commodities on the spot markets in that state. We have seen, subsequently, that the resulting Radner equilibrium allocations nonetheless replicate the Arrow-Debreu equilibrium in their results. However, we have been a bit vague about a few items which deserve further commentary. The first remark regards short-selling. Recall that to "short-sell" is effectively to borrow from future periods: namely, if afh < 0, then an agent sells security f at time t = 0 for price qf. In return, he undertakes to pay a particular amount of the unit of account (or some specific commodity or set of commodities) in period t = 1 which will be deducted from his future endowment. The amount he will pay is, naturally, state-dependent. He pays this by selling his endowment on the spot markets and acquiring the unit of account to pay off his obligations, å fÎ Frfsafh. However, there is an implicit bound to selling short: namely, the lower bound of the consumption set, Xsh. In other words, as consumption has to be non-negative, then psesh + å fÎ Frsfafh has to be non-negative for every state. If ash is negative, then it is quite possible that ½ å fÎ Frfsafh ½ > psesh, which implies, that the budget constraint in state s is such that psxsh < 0, i.e. consumption in state s Î S must be negative. This, of course, is economically ludicrous but nonetheless mathematically possible. To rule such situations out, Radner (1972) imposed a lower bound to selling short, i.e. he proposed that there is a b Î RF , such that b < ah for all h Î H. The next set of remarks regards the asset structure of the economy. This refers to the time-and-spanning properties of the assets that are made available in any particular Radner economy which can be summarized by their payoff structures. Different types of assets (bonds, stocks, etc.) can be distinguished from each other by their payoff structure. Assets can pay in real goods (e.g. bundles of commodities) or they can pay in a numeraire good (e.g. "gold") or some unit of account (i.e. "money"). Table 1 gives a heuristic idea of different assets and their payoffs in different states. We have divided this sample of assets roughly into assets which have payoffs of specific "real" commodities and assets whose payoffs are in terms of a numeraire good or unit of account.
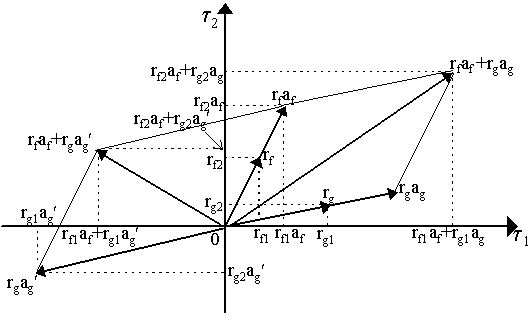
A few more words of explanation may be required to understand Table 1. Let us begin with those assets which offer specific commodities as payoffs. The first is a real asset which pays out different bundles of commodities in different states (we denote by xs the bundle received in state s). Thus, an agent who bought a "real asset" will receive delivery of a bundle of goods. An example of a real asset would be, for instance, a garden, which might deliver different combinations of cabbage, carrots, strawberries, etc. in the future depending on the state that emerges (e.g. weather). The next two categories are merely special cases of real assets. The simplest is a commodity future which pays a unit of the ith good in every state. Thus, an agent who wished to have a sure delivery of xi units of good i could purchase xi units of this commodity future. An Arrow-Debreu state-contingent claim is a special kind of commodity future: it pays a unit of a particular good i if state s emerges and nothing otherwise. Notice that this is precisely what was being implicitly purchased by agents in the Arrow-Debreu economy with full state-contingent markets: an agent who sought to receive amount xis of good i in state s would, in effect, purchase xis units of this asset. Thus, in general, in an Arrow-Debreu economy, we would we would need n(S+1) types of assets like these. Moving onto those assets with payoffs in the numeraire good or unit of account, we turn first to the most general: a numeraire asset which pays r s units of the numeraire good if state s emerges; note that it pays different amounts of the numeraire good in different states. Many types of securities fulfill this criteria. A special case of this is the riskless bond which pays a coupon, or sure amount, r of the numeraire good in every state. As an even more special case, we have the famous Arrow securities - so named because they were introduced by Kenneth J. Arrow (1953) as a substitute for state-contingent commodity claims. Arrow securities are assets which pay a single unit of the numeraire good if state s emerges and nothing otherwise. Equity shares are slightly more complicated: let q denote the percentage of a firm that a single share represents and let psys denote the profits in state s of the firm in which this share is held (expressed in terms of the numeraire good). Then, q psys is the share's payoff when state s occurs. Finally, the (European) call option is a derivative asset on another security. Defining a particular "strike-price" as c, then a call option gives the agent the option to buy, in state sÎ S, a unit of the primary asset at price c. The payoff on the primary asset in state s will be denoted r s. A call option will be exercised if r s > c - thus, the return on the option in state s is max[0, r s - c]. Any of these types of assets can be used by agents to transfer purchasing power across time and states. The set of assets available at time t = 0 which can be bought or sold, or the "asset structure" of an economy, will determine the extent to which agents can transfer purchasing power across states. However, we must be clear as to what "purchasing power" means. Notice that so far we have been carefully using the word "payoff" and not "return" in describing different assets. This is a crucial distinction because the return to an asset is the monetary value of the payoff in a particular state. Thus, a commodity future may have a payoff of xi units of commodity i in every state, but the value of that payoff in state s, the actual transfer of purchasing power, depends on pis, the spot price of commodity i state s. Thus, the return of that security in state s is pisxi and a different state which has a different spot price for good i will therefore have a different return, i.e. it may be that pisxi ¹ pis¢ xi for two states, s, s¢ Î S. We shall denote by rfs the return to asset f in state s. Thus, if we let r fs be a generic term for the "payoff" to security f in state s (whether a commodity vector or a vector with only the numeraire good), and ps the vector of spot prices in state s, then the return to security f in state s is rfs = psr fs and this is, properly speaking, the actual "income" or "purchasing power" that asset f delivers in state s. [Note: we use the term return here to refer to monetary payoff and not in the sense which the term is used in finance (which we call elsewhere "financial return"), which is defined as monetary payoff minus purchase cost over cost] One of the crucial requirements for the equivalence of Radner equilibrium and Arrow-Debreu equilibrium is that the asset structure of an economy spans the set of states. By "spanning" we mean that a combination of assets can be used to transfer any amount of purchasing power from one state to another. This can be shown as in Figure 1 where we have two states (1 and 2) and two assets f and g. A single unit of asset f has a return rf1 in state 1 and rf2 in state 2, thus return structure rf = (rf1, rf2). Similarly, a unit of asset g has return structure rg = (rg1, rg2). In Figure 1, the returns of the assets are set as vectors in the space of a single agent's net income transfers, where the origin represents the initial endowment position of the agent, t 1 > 0 represents a gain in purchasing power in state 1, t 1 < 0 a loss of purchasing power in state 2; t 2 > 0 is a gain in purchasing power in state 2, etc. Thus, starting at 0 in Figure 1, an agent who purchases a unit of asset f with his initial endowment will increase his purchasing power in state 1 by the amount rf1 and increase his purchasing power in state 2 by rf2. If he buys af units of asset f, this is shown by the stretching of the vector rf to rfaf - where we can see that he is expanding purchasing power in state 1 to rf1af and purchasing power in state 2 to rf2af.
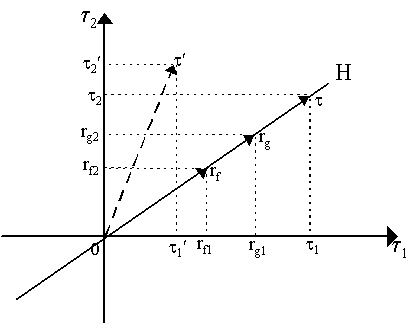
An agent can buy combinations of assets as well: purchasing af of asset f and ag of asset g, the result is the sum of the vectors rfaf and rgag, thus he can expand his purchasing power in state 1 by rf1af + rg1ag and his purchasing power in state 2 by rf2af + rg2ag. He can also achieve points in any of the negative quadrants by short-selling assets (i.e. buying "negative amounts" of asset). As shown in Figure 1, if he short-sells asset g so ag¢ < 0, then he incurs obligations to pay rg1ag¢ if state 1 occurs and pay rg2ag¢ if state 2 occurs. Consequently, if he buys af amount of asset f and short-sells ag¢ units of asset g then he can contract his purchasing power in state 1 by rf1af + rg1ag¢ and expand his purchasing power in state 2 by rf2af + rg2ag¢ . Thus, such a move would be a transfer of purchasing power between states: he would be taking part of his own endowment in state 1 and delivering it to state 2. As is evident from Figure 1, as long as the return vectors rf and rg are linearly independent of each other, then he can achieve any point in the net transfer space, i.e. he can conduct any transfer of purchasing power across states. However, this will not be true if the return vectors are linearly dependent or, more specifically, if the number of linearly independent assets in the economy is less than the number of states. This is shown in Figure 2 where we have two states and two assets, f and g, but now the returns of asset g are linearly related to the returns of asset f, i.e. rg = [rg1, rg2] = l rf = [l rf1, l rf2], where l > 0. Thus, the return vectors rf and rg lie on the same ray from the origin.
In this case, buying any quantity or combination of assets f and g will restrict the agent to the hyperplane H that passes through both vectors r f and r g. With these assets, the agent can achieve any net income transfers on this hyperplane such as t = (t 1, t 2) in Figure 2, but he cannot achieve net income transfers off the hyperplane, such as t ¢ = (t 1¢ , t 2¢ ). There is simply no way of stretching and adding these two vectors to obtain point t ¢ as a result. Consequently, the set of assets in this case does not "span" the entire state returns space. We have here what is called incomplete markets - the analysis of which we shall return to later.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
All rights reserved, Gonçalo L. Fonseca