|
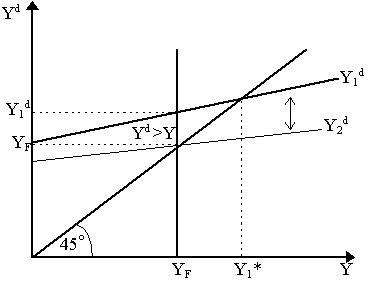
Contents (A) Demand-Pull and Cost-Push Inflation As noted earlier, one of the of the major issues facing the Keynesians in the 1950s was the issue of falling money wages. Following Modigliani (1944), they believed the Keynesian model of unemployment equilibrium could only be "closed" by assuming rigid money wages - otherwise the Keynes and Pigou effects would drive it back to full employment. But how is one to justify holding money wages rigid? The simplest solution was to appeal, as many did, to labor market imperfections, money illusions, etc. All these thoughts were pretty scattered until they stumbled across Alban W. Phillips (1958) simple diagram empirically relating money wage growth and unemployment - the infamous "Phillips Curve". The Neo-Keynesians realized immediately that this was what was necessary to "close" the Keynesian model - and consequently, Richard Lipsey (1960) and Paul Samuelson and Robert Solow (1960) integrated the "Phillips Curve" into the Neo-Keynesian edifice. The Phillips Curve also served a second purpose - namely, to provide an explanation of "inflation". Many Neo-Keynesians were living under the gnawing suspicion that Keynes's theory was a theory of "recessions" that could not be easily transferred to explain "inflationary" situations, when aggregate demand conditions were pushing the economy beyond its full employment capacity. To a good extent, they were correct: Keynes General Theory (1936) concentrated almost exclusively on underemployment equilibrium and avoided discussions of what happens beyond full employment. However, Keynes's ruminations on inflation in his How to Pay for the War (1940) gave clear indications of how to integrate inflationary pressures into his theory, but he died before he had a chance to set these down more systematically. Abba Lerner (1944, 1947, 1949, 1951) was perhaps the first Keynesian economist to stress the possibility and importance of inflation in the Keynesian model. Recall that in his theory of functional finance, Lerner made controlling inflation (and deflation) a central objective of public policy - and later formulated some rather innovative ways by which a government could do so. Perhaps more significantly, Lerner had hit on the notion of the unemployment-inflation trade-off of the Phillips Curve and the possibility of stagflation long before these were taken up by the rest of the profession in the 1960s and 1970s. (A) Demand-Pull and Cost-Push Inflation The Phillips Curve was an empirical phenomenon looking for a theory and, around that time, there were two competing theories of inflation, both of which were expressed by Keynes in various places: "demand-pull" inflation and "cost-push" inflation - terms, as Machlup (1960) has shown, that can have a far from obvious meaning. As originally expressed by John Maynard Keynes (1940) and Arthur Smithies (1942), "demand-pull" (or "inflationary gap") inflation is generated by the pressures of excess demand as an economy approaches and exceeds the full employment level of output. Output, recall, is generated by aggregate demand for goods - thus, whatever aggregate demand happens to be, aggregate supply will follow by the multiplier. However, at full employment output, if aggregate demand rises, output cannot follow because of full employment constraints. Consequently, with the multiplier disabled, the only way to clear the goods market, then, is by raising the money prices for goods. However, this is only a one-time increase in prices; inflation implies a sustained recurrent increase in prices. Keynes and Smithies explained inflation proper by appealing to distributional effects. The Keynes-Smithies story can be expressed in the 45° income-expenditure diagram in Figure 11 where YF is full employment output and Y1d is aggregate demand. Note that the market-clearing level of output is Y1*, but it is not achievable - thus the "inflationary gap" is the difference between YF and Y1*. Keynes's (1940) argument can be restated as follows: as money wages lag behind good prices in adjustment, the rise in prices will therefore lead to a distribution of income away from wage-earners and towards profit-earners. He posited that, as workers have greater marginal propensities to consume than profit-earners, the redistribution of income induced by the inflationary gap will thereby lead to lower aggregate demand and thus close the gap, i.e. the aggregate demand curve flattens and falls in the Figure 11 from Y1d to Y2d .
The problem, of course, is that workers' money wages will still adjust upwards (recall that they were lagged behind), consequently once these adjust, income is redistributed away from profit-earners and towards wage-earners so that demand rises again (from Y2d to Y1d in Figure 11) and thus the inflationary gap re-emerges. But that inflationary gap, as noted earlier, leads to another price rise, redistribution of income to profiteers, etc. Thus, the whole process repeats itself continuously so that there will be, effectively, sustained, continual increases in prices, i.e. inflation. In contrast, the "cost-push" theory of inflation or "sellers' inflation", also suggested in Keynes (1940), was more in line with older Marxian and Kaleckian sources - although this notion was also shared by Keynesian economists (e.g. Abba Lerner, 1951; Nicholas Kaldor, 1959; Sidney Weintraub, 1959) and Neoclassical economists (e.g. Milton Friedman, 1951). The basic notion is that, in a generally imperfectly competitive economy, firms set prices of output according to a simple mark-up formula:
where m is the mark-up, p price and w wage. When an economy approaches full employment, the "reserve army of the unemployed" gradually disappears, labor's hand at the bargaining table is strengthened. This will embolden laborers or their representatives to demand an increase in wages. In order to prevent this wage increase from eating into profits, employers will subsequently raise prices and keep the mark-up intact. Of course, if this happens, then workers will not be making any real wage gains. Perceiving this, they will follow up with another round of nominal wage increases - which in turn will be followed by a price increase and so on. Thus, in this version, inflation is a result of this wage-price spiral engendered by the relative bargaining position of workers in an almost fully employed economy. Incomes policies, which would link wage increases to rises in productivity, were suggested by many economsts (e.g. Lerner, 1947; Weintraub and Wallich, 1971; Okun and Perry, 1978) as a way of combating this type of inflation. However, as Lerner (1951, 1972) stresses, the blame for inflation need not be placed squarely on the shoulders of workers alone: a push for profits by owners will be enough to initiate this kind of price-wage inflation spiral. In particular, there might be such a push when the owners' bargaining position seems relatively strong, i.e. when unemployment is high. Consequently, Lerner recognized the possibility of inflation with high unemployment, i.e. stagflation. It was precisely to combat this type of inflation that Lerner and Colander (1980) introduced their novel "Market Anti-Inflation Plan" (MAP) in the stagflationary 1970s: specifically, they proposed that the "right" to change prices be assigned to firms in the form of a fixed supply of tradeable vouchers, so that if a firm attempts to raise its prices, it would have to cash in its vouchers and thus relinquish its right to further price increases (whereas a firm which lower prices would gain vouchers). If a particular firm remained intent on raising prices further, then it would have to purchase vouchers from other firms on the open market. In their view, these added costs would make a profit-induced price rise less appealing to firms and thus help bring stagflation under control. Both the "demand-pull" and "cost-push" theories of inflation are reconcilable with the empirical phenomena summarized by the Phillips Curve: as unemployment approaches zero, wage inflation (and price inflation) rises. However, the theories are different in that the first theory stresses more demand-side considerations while the latter concentrates more on supply-side. The corresponding "solutions" to the inflation problem are also different: "demand-pull" theorists concentrate on bringing down demand by, for example, reducing government expenditure, while "cost-pushers" call for the alleviation of wage pressure by institutional reform or incomes policies. Although acknowledging the possibility of "cost push", most Neo-Keynesians took up the demand-pull explanation of inflation. However, the Keynes-Smithies story was told almost completely in the context of income and expenditure, and thus, surprisingly, ignored the monetary side. The Neo-Keynesians nonetheless attempted to appropriate the story into their IS-LM model by simply grafting on a capacity constraint, YF, to the left of the IS-LM-determined equilibrium, Y* and calling the resulting difference the "inflationary gap". With output stuck at YF, excess demand for goods will result in increases in the price level as before. However, unlike the Keynes-Smithies story, there is not a resulting "redistribution" of income to close the gap. Rather, as price level rises, the real money supply collapses and thus the LM curve shifts to the left and thus back to full employment output. Thus, the transmission mechanism implies that any price rises will themselves close the gap by lowering money supply and thus increasing interest rates and thus reducing investment and demand. However, with the LM curve moving to bring the economy to full employment, it seems impossible, in this case, to have sustained price rises (i.e. inflation) as the monetary side seems to close off the story entirely. One could subsequently argue that, as real wages (w/p) declined in the process, then workers would try to bid their money wages back up and thus regenerate the gap. However, recall that from the four-quadrant IS-LM diagram (our earlier Figure 4), when IS-LM centers on the full employment output level so that Y* = YF, then the labor market clears and thus there are apparently no inherent dynamics to imply a rise in wages. If anything, a Pigou Effect arising from the fall in real money balances ought to push the IS curve to the left and actually generate unemployment so the implied dynamic might actually be a fall in money wages (of course, in the process of the original adjustment, IS and LM could move concurrently to the left and land at YF together, but then we are back to a full-employment centered equilibrium). In short, in an IS-LM context, we can obtain price rises but, at least within the confines of the model, we cannot obtain continuous inflation unless aggregate demand rises again for some reason - and there is no apparent reason why it will do so. The problem, of course, returns to the old issue of what happens in that mysterious labor market which was so murky in the Hicks-Modigliani IS-LM world. The Keynes-Smithies story has workers bargaining for money wages upwards in response to the rise in prices, and the IS-LM story can accommodate that explanation, but it requires grafting on a theory of the labor market money wage bargain into the IS-LM model. One of the first attempts to consider both labor market dynamics and goods market dynamics within one model was Bent Hansen's celebrated "two-gap" model (B. Hansen, 1951). Nominal wage movements are governed by the disequilibria in the labor market while nominal price movements are governed by disequilibria in the goods market so that the dynamics of the real wage and inflation arise from the interaction of the both goods and labor markets. However, the ideas of sustained disequilibrium "gaps" and price movements adjusting goods markets - with full employment - sound more Wicksellian than Keynesian. And it ought to - for Bent Hansen was a bona fide Wicksellian and his 1951 effort could be thought of as the swan song of the dying Stockholm School - or the opening notes of the disequilibrium "Walrasian-Keynesian" school - and thus not properly part of the Neoclassical-Keynesian Synthesis. (B) The Phillips Curve When the Neo-Keynesians decided to incorporate labor market dynamics into their IS-LM model, the empirical Phillips Curve provided the excuse and the troublesome money wage left hanging in Chapter 19 of Keynes's General Theory (1936) provided the incentive. The Phillips Curve relates money wage inflation to unemployment in the following general fashion:
where h¢ < 0 so that as unemployment increases, then wage inflation declines. Tying price movements one-for-one to wage movements, then this could be rewritten:
so that price inflation was negatively correlated with unemployment. The Phillips Curve is shown in Figure 12. The theoretical argument provided by Richard Lipsey (1960) was based largely on Neoclassical micro theory transferred to macroeconomics and formulated in the tradition of the "demand-pull" theories. Effectively, Lipsey argued that if labor markets for a particular industry were in disequilibrium, then the speed at which (nominal) wages adjust depends on the ratio of the difference between labor demand and supply to the supply of labor, i.e.
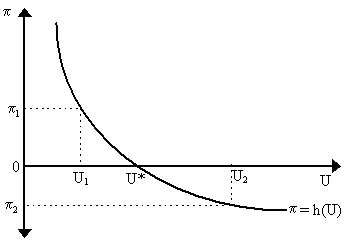
where ¦ ¢ > 0 so, thus, the larger the excess demand for labor in this industry, the faster the rate of adjustment of the money wage. As (Ld - Ls)/Ls = -U, then the rate of growth of money wages in this industry is negatively related to unemployment in this industry. If there is no productivity growth, then for profit-maximizing firms, the real wage should be constant, so that (dw/dt)/w = (dp/dt)/p thus inflation, p , is negatively related to the unemployment rate - the Phillips Curve relationship, p = h(U) (we can translate ¦ = -h). The non-linearity of the Phillips Curve is justified by appeals to frictional unemployment and institutional difficulties at the extremes.
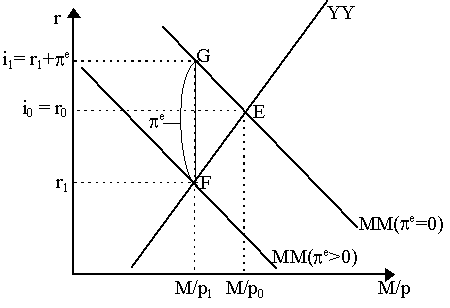
However, what is not satisfactory in this explanation is how a level of inflation and unemployment can be sustained at positive amounts. The microeconomic theory, after all, suggest that eventually equilibrium will be reached and unemployment eliminated. Positive unemployment can possibly be justified on the basis of frictional issues (workers changing jobs, etc.), but positive inflation, as the equation above indicates, relies on a persistent excess demand for labor. The solution for the Neo-Keynesians was actually quite simple: aggregate the Lipsey micro story and then trace out the implied macroconstraints. Effectively, by aggregating the industry-level Phillips Curves, we obtain an aggregate or "average" Phillips Curve of effectively the same shape. However, relative to the industry-level Phillips curve, the average Phillips Curve will actually be shifted upwards to the right. The reason is due to the distribution of unemployment across industries and the non-linearity of the underlying industry-level curves. Suppose there are two industries with identical Phillips Curves (thus both have industry-level Phillips Curves as in Figure 12) and suppose that one faces unemployment U1 and the second faces unemployment U2 and suppose, for the sake of argument, that (U1 + U2)/2 = U* so that average unemployment coincides with U*. For any individual industry, being at U* implies that p = 0. However, in the average, being at U* implies that p > 0. The reason is that, because of the non-linearity, p1 > -p2, so that the average inflation rate is positive, (p1 + p2)/2 > 0 when the average unemployment is at U*. Thus, the average Phillips Curve is actually to the right of the individual Phillips Curve even if all industry-level curves are identical. In short, the zero-inflation unemployment rate for the average is greater than the zero-inflation unemployment rate for the individual industry. Thus, actual inflation is not only a function of the unemployment level in the economy, it is also a function of the distribution of that unemployment across industries. However, we still have not answered our question: how do we obtain persistent excess demand and thus persistent inflation? The logic, at the individual level, is that if there is excess demand in a particular industry, wages rise to attract workers from other industries. As these workers arrive, the adjustment will be towards equilibrium and thus industrial-level excess demand is eliminated. In the aggregate economy, however, there is no pool of workers forthcoming as we are above full employment. Thus, excess demand persists in the aggregate and is not eliminated by the wage adjustment process. The next question imposes itself: if wage rises do not eliminate excess demand, why posit such a process at all? Again, this resolves itself by disentangling individual-aggregate reasoning: in particular, firms will raise wages when there is excess aggregate demand in order to poach workers from other industries, and the other industries will raise wages to avoid their workers being lured away. Thus, although the economy as a whole will not call forth more laborers in the aggregate by raising wages (although some of the voluntarily unemployed might be tempted to join the labor market), individual firms have a rationale to raise wages regardless. Thus, in aggregate, persistent inflation can occur. Lipsey's (1960) theoretical justification of the Phillips Curve seemed to make its integration in macro theory amenable to the Neo-Keynesians. Not only was the issue of money wages finally hung on a peg (albeit shifted by a derivative), but inflation was brought into the Keynesian apparatus. What made the whole enterprise all the sweeter was the nice policy conclusions that could be derived. As emphasized by Paul Samuelson and Robert Solow (1960), if the Phillips Curve were seen as a stable empirical relationship between unemployment and inflation, then a policy-maker could find the particular rate of unemployment (U*) needed for price stability (p = 0). Alternatively, if the policy-maker wanted to achieve a higher level of employment (thus lower unemployment, say at U1 in Figure 12), then he would have to allow for inflation at p1. (the converse case of deflation and high unemployment are seen at U2, p2). In short, Samuelson and Solow (1960) argued that there was a definite inflation-unemployment trade-off which could be manipulated by policy-makers. So, from Phillips' simple 1958 results, not only was Neo-Keynesian theory "completed" but impressive policy conclusions were derived to boot. (C) Inflation and Interest Rates The Neo-Keynesians went to some great efforts to incorporate inflation into their world, and they duly believed that much was gained in terms of closing their model and engendering new policy perspectives. But the next question seemed to be a more pertinent one: what are the implications of inflation on the workings of the rest of the model? In fact, not many. The only thing highlighted by the introduction of inflation was the effect on interest rates as outlined by Robert Mundell (1963) and Roy Harrod (1969). Mundell tackled the old Fisherian law on the constancy of the real rate of interest, i.e. where r = i - p where if inflation (p) rises, then nominal interest rate (i) will rise one-for-one to keep real interest rates (r) constant. Keynes (1936), of course, disputed Fisher's assertion and Fisher (1930) himself was reluctant to make too much out of it empirically. Mundell (1963) advanced on them both by proving that it was invalid in an IS-LM type of model. Mundell's reasoning was as follows: the nominal rate of interest is set by inflation expectations and the real interest rate, i = r + pe. Now, suppose we have two assets, money and equity, where r is the real return on equity. By Keynes's theory of liquidity preference, money demand is inversely related to the return on alternative assets, i.e. L(r, Y). We know, of course, that in equilibrium M/p = L(r, Y), as money supply rises, the rate of interest falls, so we can trace out an money market (MM) equilibrium locus in interest/money supply space as in Figure 13. Now, a particular MM curve is conditional on a particular level of inflationary expectations (pe). If inflationary expectations rise, then, for any given amount of money supply, the real interest rate, r = i - pe, falls and thus the MM curve shifts down. The intuitive logic is that we must remember that the negative of inflation is the real rate of return on money. Thus, if there are inflationary expectations, agents who hold money are receiving a negative expected return on their real balances and thus will attempt to get rid of them by purchasing equity. As a result, money demand falls and the price of equity rises - and consequently the real rate of return on equity, r, falls. In Figure 13, we denote by MM(pe=0) the money market equilibrium locus where there are no inflationary expectations and MM(pe > 0) as the money market equilibrium locus when there is a particular positive expected inflation rate. However, recall also from simple analysis, that real interest rates impact the goods market as well.. Making use of some Neo-Keynesian transmission mechanisms, as r rises, consumption falls and investment falls. Furthermore, recall that by a Pigou Effect, a rise in money supply increases net wealth and hence consumption. Thus, consumption can be summarized by C = C(r, Y, V) where Cr < 0, CY > 0 and CV > 0. The term V is aggregate net wealth, here defined as V = E + M/p (where E is equity and M/p the real money supply). Investment is I = I(r) where Ir < 0 by the marginal efficiency of investment story. In goods market equilibrium, aggregate demand equals aggregate supply, so Y = Yd = C(r, Y, V) + I(r). Thus, we can draw out a YY curve which denotes the relationship between money supply M/p and interest. Specifically, note that as r rises, investment and consumption falls, so in order to keep the same level of output, then, money supply must rise. Thus, the YY equilibrium locus (which is for a given level of output) is upward sloping in money supply-interest rate space, as shown in Figure 13.
Suppose, now, that inflationary expectations are zero, pe = 0, so the MM(pe = 0) curve applies. Goods market and money market equilibrium implies that we achieve equilibrium E where money supply is M/p0 and real and nominal interest rates are equal to each other at i0 = r0. We can now trace out the consequences of an exogenous increase in inflationary expectations. By raising inflationary expectations to some positive amount, pe > 0, the MM curves shifts down to MM(pe >0). The new equilibrium rate of real interest, r1, is at point F in Figure 13, where MM(p e>0) and YY intersect. However, as now i = r + pe, then a "wedge" of size pe is created between the old MM curve and the new one: the new real rate r1 is read off the intersection of YY and the new MM curve (point F) and the new nominal rate i1 is read off the top curve MM(pe=0) at the same level of money supply (point G). Obviously, then, the introduction of inflationary expectations has increased the nominal interest rate from i0 to i1, but the amount of the increase is less than the full amount of expectations, pe. In other words, the real rate of interest has fallen by less than the full amount of inflationary expectations. Thus, Fisher's Law of nominal interest rates adjusting to inflationary expectations one-for-one is disabled. What is happening, intuitively? A higher expected rate of inflation drove up the nominal rate. This, consequently, made equity more attractive relative to money. Consequently, agents attempted to get rid of their excess money holdings by bidding up the price of equity and thus drove the real rate of return on equity down. This collapse in the real rate of return will induce more investment, but as we are at a fixed level of output, then consequently something else must give way to keep aggregate demand constant - namely, consumption. We do this by bringing the money supply down from from M/p0 to M/p1 and so, by the Pigou Effect, consumption falls and thus aggregate demand returns to its initial level. The reason why nominal rates did not rise one-for-one with inflationary expectations was due to the portfolio shiftings of households away from money and towards equity, which drove its real rate down This effect was not anticipated by Irving Fisher in the original Neoclassical loanable funds story - although it could be incorporated in it. Thus, the alternative "loanable funds" interpretation of the Mundell story would be that agents increase demand for capital but since capital cannot be increased, this will raise prices, which will lead to a collapse in the money supply which, by the Pigou Effect, reduces consumption and increases savings, consequently reducing the required rate of return on capital and thus bringing investment back up. Of course, it might be possible to restore the original Fisher effect by allowing banks to pay interest on deposits. In this case, the fall in the return on money (i.e. inflation) could be compensated one-for-one with a rise in the return on deposits - thus leaving people happy enough with the existing portfolio. Furthermore, as Edmund Phelps (1965) demonstrates, strange things can happen when we add a government to the story and make inflationary expectations endogenous to an increase in money supply. Suppose the government increases money supply in order to finance an expansionary fiscal deficit. Then, aggregate demand rises to Yd = C(r, Y, V) + I(r) + G. If output is to be the same, then either r must rise or M/p fall - thus the YY curve must shift to the left. As a result, any inflationary expectations induced by the government action, which shift the MM curve down, may or may not decrease the real rate of interest - it depends on the relative size of the shifts. However, if money supply rises via open market operations, then equity holdings are reduced and thus the IS curve will shift to the right by the real-balance effect and thus the inflationary expectations-induced fall in MM will reduce the real rate more than if the government was not involved. In sum, Mundell's (1963) proposition was that inflation (rather, inflationary expectations) will have real effect on the economy by inducing people to move away from money and towards capital. James Tobin (1965) incorporated Mundell's proposition in his famous monetary growth model and obtained the result that inflation could have a positive influence on growth if it induced people to move away from money and towards capital accumulation. This effect of inflation and inflationary expectations on portfolio balances has since become known as the "Tobin-Mundell" effect and was used by James Tobin (1975, 1993) and Bradford de Long and Larry Summers (1986) to counter the claim that price flexibility would draw the Keynesian unemployment equilibrium towards full employment. Namely, with deflation induced by labor market conditions, the return on money increases and so, by deflationary expectations, agents will move away from illiquid assets and towards money - thereby increasing money demand and pushing the LM curve to the left, reducing output further. Thus, wage and price flexibility in unemployment situations could easily lead to more as opposed to less unemployment. (D) The Expectations-Augmented Phillips Curve The Phillips Curve did well for a while - but all this changed in the 1970s, a period of high unemployment and high inflation. This phenomenon was obviously incompatible with the received reasoning of the Phillips Curve. How then is one to explain this? One way, followed by many Keynesians, was simply to argue that the Phillips Curve was "migrating" in a northeasterly direction, so that any given level of unemployment was related to higher and higher levels of inflation. But why? Certainly, there were many explanations for this - and all quite imaginative. It was the subequent observation that was disturbing: if the Phillips Curve is indeed migrating, then the relationship between inflation and unemployment is not really a negative one. As the major justification for the Phillips Curve was largely its empirical veracity and not a theoretical derivation, then what is the point of the Phillips Curve when it is no longer empirically true? More pertinently for policy-makers, a migrating Phillips Curve is clearly not policy-effective: with the Phillips Curve shifting around, then the inflation cost of targeting a particular unemployment rate is not clearly identifiable. Milton Friedman (1968) and Edmund Phelps (1967) rose to the occasion to propose an expectations-augmented Phillips Curve - which was then incorporated into the Neo-Keynesian paradigm by James Tobin (1968, 1972). The Neo-Keynesian story can be thought of as follows: let aggregate nominal demand be denoted D, so that D = pY. Dynamizing, then:
or, letting gD = (dD/dt)/D and accordingly for the other parameters and letting inflation gp be denoted p , then we can rewrite this as:
so price inflation is driven by nominal demand growth (gD) and output/productivity growth (gY). Now, assuming the standard Keynesian labor market condition that the marginal product of labor is equal to the real wage (w/p), then dynamizing this:
where gw is nominal wage growth, so the marginal productivity rule is applying dynamically. Expressing for p and equating with our earlier term then we can obtain:
i.e. nominal wage inflation is equal to nominal aggregate demand growth. Now, the Friedman-Phelps proposition for expectations augmentation was proposed as:
so wage inflation is negatively related to the unemployment rate (U), so that h' < 0 as before, positively to productivity growth (so a > 0) and positively with inflation expectations, pe (so b > 0). Let us, temporarily, presume productivity growth is zero so that gY = 0. In this case, gw = p (so note that the real wage is constant) so that this can be rewritten:
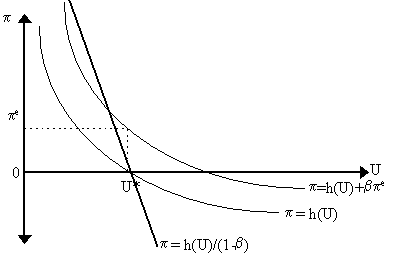
which is simply the expectations-augmented Phillips Curve, as shown in Figure 14. The term b is the expectations augmentation parameter (specifically, b is the speed at which expectations are adjusted to actual experience). Thus, pe = 0 (expectations of zero inflation), we have our old p = h(U) curve unchanged. But if there are positive inflationary expectations (pe > 0), then this curve shifts upwards, as shown in Figure 14. The relationship between inflationary expectations and wage inflation is explained in terms of the labor market bargaining process. If workers expect inflation to increase, then they will adjust their nominal wage demands so that gw > 0 and thus p > 0. It is assumed, in this paradigm, that 0 < b < 1 - not all expectations are carried through. So, for each level of expectations, there is a specific "short-run" Phillips Curve. For higher and higher expectations, the Phillips Curve moves northeast. Thus, the migration of the so-called "short-run" Phillips Curve (as in the move in Figure 14) was explained in terms of ever-higher inflationary expectations. However, for any given level of expectations, there is a potential trade-off (as a matter of policy) between unemployment and inflation.
So much for the short-run. What about the long run? In the Friedman-Phelps argument, the long-run can be defined where expectations of inflation are equal to actual inflation, i.e. p = pe, in other words, the expectations of inflation in the next period are equal to the actual inflation of this period. Thus, we can input this into the expectations-augmented Phillips Curve relationship so:
or, simply rearranging:
which is the long-run Phillips Curve relationship. The long-run inflation-unemployment trade-off can be found simply by the slope:
where, since h' < 0 and if b < 1, this implies that dp/dU < 0. In other words, in the long run, inflation is still negatively related to the unemployment rate (the shape of the Phillips Curve) albeit steeper than the simple short-run Phillips curve (which had slope h¢ ). The intuitive explanation is simple. In the short-run, where expectations are given, a fall in unemployment due to an increase in nominal demand leads to a rise in inflation. This rise comes from the h component of the Phillips curve alone. However, with expectations far more flexible in the long run, a drop in unemployment will again lead to inflation but this rise will be reinforced by higher inflationary expectations. Thus, the rise in inflation will be carried through by the h component and the pe component. Thus, in the long-run, the trade-off becomes steeper. What if we include productivity growth back in, i.e. let gY > 0? In this case, our original short-run wage inflation function is:
so, for the long run, let p = pe again and input our earlier expression for inflation (p = gw - gY), so that:
or simply:
The long-run trade off between wage inflation and unemployment is still dgw/dU = h'(U)/(1-b) < 0 if we assume h¢ < 0 and b < 1. So what about productivity? Well, if a is small and b large enough so that (a -b) > 0, then productivity growth gY leads to wage inflation. If, on the other hand, (a -b) < 0, then a rise in productivity will lead to a fall in wage inflation. The first case is clear, the last case less so, but it is easily explained. Workers can respond in various ways to productivity growth. It is assumed that they will want their real wage, w/p, to increase. They can do so in two ways: firstly, by having their nominal wages increase or, alternatively, by letting prices decline. Either way, the real wage w/p rises in response to productivity. However, given that this equation considers only nominal wage inflation, then the (a - b) parameter matters in the transmission of productivity improvements. Returning to our original discussion, as long as b < 1, such that dp/dU < 0, then we get a negatively-sloped long-run Phillips curve as shown in Figure 14. If, however, b = 1 so that all expectations are fully carried through, then dp/dU = ¥ , the long-run Phillips Curve is vertical. This latter case was the proposition insisted on by Phelps (1967) and Friedman (1968) and forms the core of the "Monetarist Critique". The vertical long-run Phillips Curve implies, then, that there is no long-run output-inflation trade-off and that, instead, a "natural rate of unemployment" will prevail in the long-run at the intercept of the long-run Phillips Curve with the horizontal axis. Note that this "natural rate" hypothesis was suggested before the complete breakout of stagflation in the 1970s - although that was famously predicted by Milton Friedman (1968) in his Presidential Address to the American Economic Association (AEA). Taking up the Neo-Keynesian mantle, as he had done so many times before, James Tobin's response in his own 1972 AEA presidential address, was to insist on b < 1 strictly. The logic Tobin offered was that in some industries, where unemployment is high, the expectation of higher inflation will not be carried through to proportionally higher wage demands. Quite simply, workers in high unemployment industries, realizing that they are quite replaceable, will not want to risk getting dismissed by demanding that their real wage remain unchanged. Instead, they might accept a slight drop in their real wage, grit their teeth and bear it - at least until the reserve army of labor (i.e. the unemployed) begins to disappear or better opportunities arise elsewhere. Thus, their expectation of inflation does not get translated into a proportional wage demand, consequently b < 1. Only if their industry is at or near full employment, then they will be bold enough to ask for a proportional increase in wages. In Tobin's (1972) multi-sector reasoning, which followed up on Archibald (1969), at any point in time, unemployment is unevenly distributed across industries so that some firms are at full employment (so b = 1) and others are at underemployment (b < 1). Therefore, the aggregate b < 1 can be justified by the distribution of unemployment across different sectors. Over time, of course, the unemployment distribution will change as workers receive better information and the composition of aggregate demand and the structure of the economy changes. However, as there will always be uneven distribution, the aggregate, long-term Phillips Curve will still be downward-sloping. However, Tobin's argument apparently did not convince and the Monetarist hypothesis of a vertical long-run Phillips Curve (with its associated "natural rate of unemployment") converted many economists and, eventually, policy-makers. In the 1970s, even this was displaced when the New Classicals proposed that, due to rational expectations, the short-run Phillips Curve was also vertical. Thus, in the New Classical view, there is no involuntary unemployment, in the short-run or the long-run. Unemployment would be stuck at its natural level at all times. They justified long spells of high unemployment on the basis of changes in the "natural rate" which were largely external to the model (e.g. because of a greater preference for leisure, higher search costs, higher unemployment benefits, worse information, institutional rigidities and other exogenously-imposed "distortions" or "shocks"). In the wake of the Monetarist and New Classical counter-revolutions of the 1970s, many economists had to run quite some miles to rescue at least the downward-sloping short-run Phillips Curve or argue for a migratory pattern for the natural rate of unemployment. Innovative arguments based on efficiency wages, menu costs, etc. were pursued by a school of economists calling themselves "New Keynesians". However, our story must end now - for the phenomena the New Keynesians concentrate on are not only "imperfectionist" (and thus contrary to Keynes's methodology) but, above everything, their explanations are wholly grounded in supply-side conditions. In the New Keynesian theories, the notion of an effective demand-determined equilibrium is absent. As a result, they cannot, by any stretch of the imagination, be considered part of the "Keynesian" world.
|
All rights reserved, Gonçalo L. Fonseca